Cartesian Coordinates
The Cartesian Coordinate system
The cartesian 3d coordinate system
There are several common ways to express a location:
\begin{align}
\mathbf{a} & = a_x \hat{\bf{x}} + a_y \hat{\bf{y}} + a_z \hat{\bf{z}}\\
& = a_x \hat{\bf{i}} + a_y \hat{\bf{j}} + a_z \hat{\bf{k}}\\
& = (a_x,a_y,a_z) \\
& = a_1 \mathbf{e}_1 + a_2 \mathbf{e}_2 + a_3 \mathbf{e}_3 \\
& = \sum_{i=1}^3 a_i \bf{e}_i \\
& = \begin{bmatrix}
x_1 \\
x_2 \\
x_3
\end{bmatrix}
\end{align}
In a 3d world, we can describe the position of any point using 3 coordinates.
This of course is a vector !
Magnitudes
$a^2 + b^2 = c^2$
Addition & Subtraction
$$\mathbf{a} = a_1 \hat{\bf{x}} + a_2 \hat{\bf{y}} +a_3 \hat{\bf{z}}
$$
And
$$\mathbf{b} = b_1 \hat{\bf{x}} + b_2 \hat{\bf{y}} +b_3 \hat{\bf{z}}
$$
then,
$$\mathbf{a} + \mathbf{b} = (a_1+b_1) \hat{\bf{x}} + (a_2+b_2) \hat{\bf{y}} + (a_3+b_3) \hat{\bf{z}}$$
and
$$\mathbf{a} - \mathbf{b} = (a_1-b_1) \hat{\bf{x}} + (a_2-b_2) \hat{\bf{y}} + (a_3-b_3) \hat{\bf{z}}$$
Dot Product
There are two ways of multiplying vectors:
1. The dot product (or scalar product)
$\mathbf{a} \cdot \mathbf{b} = a b \cos \theta$
$\mathbf{a} \cdot \mathbf{b} = (a_1 \hat{\mathbf{x}}+a_2 \hat{\mathbf{y}}+a_3 \hat{\mathbf{z}})\cdot(b_1 \hat{\mathbf{x}}+b_2 \hat{\mathbf{y}}+b_3 \hat{\mathbf{z}}) $
$\mathbf{a} \cdot \mathbf{b} = a_1 b_1 + a_2 b_2 + a_3 b_3$
Dot Product - Linear Algebra
$$
\begin{bmatrix}
a_1 \;
a_2 \;
a_3
\end{bmatrix}
\cdot \begin{bmatrix}
b_1 \\
b_2 \\
b_3
\end{bmatrix}
=
a_1 b_1 + a_2 b_2 + a_3 b_3
$$
Cross Product
Defined as:
$$\mathbf {a} \times \mathbf {b} =|\mathbf {a} | \; |\mathbf {b}|\; \sin(\theta )\ \mathbf {n} $$
where $\theta$ is the angle between $\mathbf {a} $ and $\mathbf {b}$, and $\mathbf {n}$ is the unit vector perpendicular to the plane containing $\mathbf {a} $ and $\mathbf {b}$
This produces a third vector that points perpendicular to both the original vectors.
$\mathbf{a} \times \mathbf{b} = (a_x \hat{\mathbf{x}}+a_y \hat{\mathbf{y}}+a_z \hat{\mathbf{z}})\times(b_x \hat{\mathbf{x}}+b_y \hat{\mathbf{y}}+b_z \hat{\mathbf{z}}) $
We can calculate the cross product by computing the determinant of this matrix:
$$\mathbf{a} \times \mathbf{b} = \begin{vmatrix}
\mathbf{\hat{x}} & \mathbf{\hat{y}} & \mathbf{\hat{z}} \\
a_x & a_y & a_z \\
b_x & b_y &b_z \\
\end{vmatrix}
$$
$$\mathbf{a} \times \mathbf{b} = (a_y b_z-a_z b_y)\hat{\mathbf{x}}+(a_z b_x-a_x b_z)\hat{\mathbf{y}}+(a_x b_y-a_y b_x)\hat{\mathbf{z}} $$
Mathematica:
a = {a1, a2, a3}
b = {b1, b2, b3}
Dot[a,b]
-> a1 b1 + a2 b2 + a3 b3
Cross[a,b]
-> {-a3 b2 + a2 b3, a3 b1 - a1 b3, -a2 b1 + a1 b2}
numpy (python)
import numpy as np
a = np.array([2,4,5])
b = np.array([1,-2,3])
c = np.dot(a,b)
print(c)
-> 9
d = np.cross(a,b)
print(d)
-> [22 -1 -8]
Quadratic Drag in two dimensions
In cartesian coordinates:
$$
\begin{align}
m \ddot{\mathbf{r}} & = m \mathbf{g} - c v^2 \; \hat{\bf{v}} \\
& = m \mathbf{g} - c v \; \mathbf{v}
\end{align}
$$
This, if you remember 2 kinematics from 20700, requires breaking the problem up into both directions. Previously, those two directions where independent, meaning what happens in one, stays there and doesn't affect the other. But, know, with the velocity dependent drag, they are coupled:
$$
\begin{align}
m \dot{v}_x & = -c \sqrt{v_x^2 + v_y^2} \; v_x \\
m \dot{v}_y & = -mg - c \sqrt{v_x^2 + v_y^2} \; v_y
\end{align}
$$
This is an example (already!) of something that has no analytic solution. That means we can't use separation of variable or any other regular diff.eq techniques to find a general solution to this. Numerical methods are the only way.
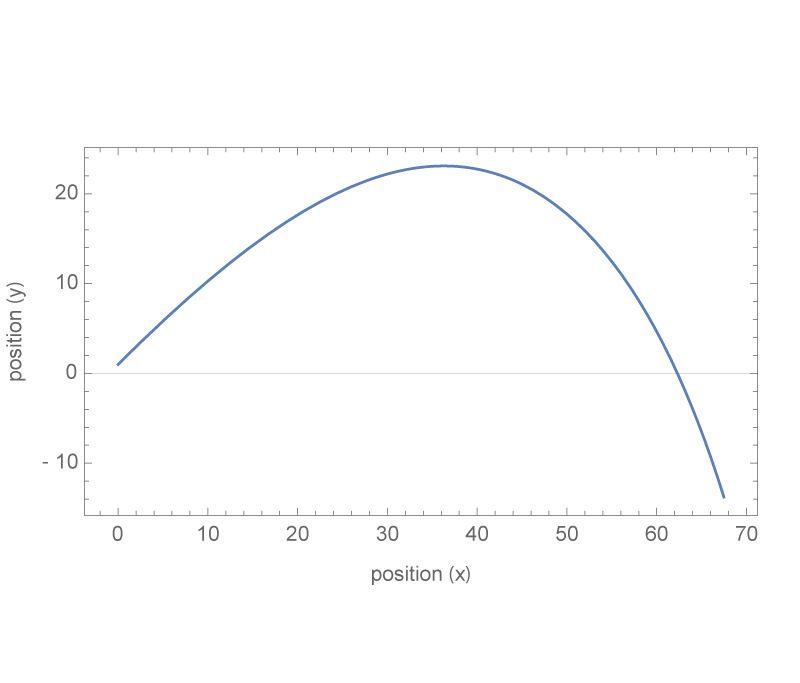
Plot motion for a projectile experiencing quadratic drag.
Mathematica:
Define some parameters
r = .05;
area = Pi r^2;
m = .15;
g = 9.8;
Cd = 0.47;
\[Rho] = 1.29;
c = 1/2 \[Rho] area Cd;
\[Theta] = Pi/4
v0 = 40;
Define our differential equations
In the x direction:
$$
m \ddot{x} = -c \dot{x} \sqrt{\dot{x}^2+\dot{y}^2}
$$
And
$$
m \ddot{y} =-m g -c \dot{y} \sqrt{\dot{x}^2+\dot{y}^2}
$$
diffeqs = {m x''[t] == -c x'[t]*Sqrt[x'[t]^2 + y'[t]^2],
m y''[t] == -m g - c y'[t]*Sqrt[x'[t]^2 + y'[t]^2],
x[0] == 0,
x'[0] == v0 Cos[\[Theta]],
y[0] == 1,
y'[0] == v0 Sin[\[Theta]]
}
Use NDSolve[] to solve them.
solutions = NDSolve[diffeqs, {x[t], y[t]}, {t, 0, 6}]
Plot x vs. y using ParametricPlot[]
ParametricPlot[{x[t] /. solutions[[1, 1]], y[t] /. solutions[[1, 2]]}, {t, 0, 5}]
Polar
The basic polar coordinate system
$$\begin{eqnarray}
x &=& r \cos \theta \\
y &=& r \sin \theta \nonumber \\
\end{eqnarray}$$
$$\begin{eqnarray}
r = \sqrt{x^2 + y^2} \\
\theta = \tan^{-1} \left(\frac{y}{x}\right) \nonumber \\
\end{eqnarray}$$
Goal: Express newton's laws in these non-cartesian coordinates:
$$ F = m\ddot{\mathbf{r}}$$
Unit vectors in polar coordinates
Unit vectors in polar coordinates
$\mathbf{\hat{r}}$ points in the direction of increasing $r$ (given a fixed $\theta$)
$\boldsymbol{\hat{\theta}}$ points in the direction of increasing $\theta$ (given a fixed $r$)
Now, the unit vectors change!
We start with $\hat{\bf{r}}$
$$
\begin{align}
\Delta \hat{\bf{r}}\ & \approx \Delta \theta \; \hat{\boldsymbol{\theta}} \\
& \approx \dot{\theta} \Delta t \; \hat{\boldsymbol{\theta}}
\end{align}
$$
Taking the time derivative:
$$
\frac{d \hat{\bf{r}}}{dt} = \dot{\theta} \; \hat{\boldsymbol{\theta}}
$$
Taking the time derivative of $\mathbf{r} = r \hat{\bf{r}}$
\begin{equation}
\dot{\mathbf{r}} = \dot{r} \hat{\bf{r}} + r \frac{d \hat{\bf{r}}}{dt}
\end{equation}
which can be used to express the velocity of the particle in polar coordinates:
\begin{equation}
\mathbf{v} \equiv \dot{\mathbf{r}} = \dot{r} \hat{\bf{r}} + r \dot{\theta} \; \hat{\boldsymbol{\theta}}
\end{equation}
This might look a little different, but you've seen it before. The components are:
$$
\begin{align}
v_r & = \dot{r}\\
v_\theta & = r \dot{\theta} = r \omega
\label{eq:rotationalvelocitycircularmotion}
\end{align}
$$
\eqref{eq:rotationalvelocitycircularmotion} is just what we had for Uniform Circular Motion , i.e. when $r$ wasn't changing. Now we have to account for changing $r$ values, so we really need both terms.
Velocity expressed in polar coordinates:
\begin{equation}
\dot{\mathbf{r}} = \dot{r} \hat{\bf{r}} + r \dot{\theta} \; \hat{\boldsymbol{\theta}}
\end{equation}
Now we need to get the acceleration
To find the acceleration, we know have to take the time derivative of the velocity:
\begin{equation}
\mathbf{a} \equiv \ddot{\mathbf{r}} = \frac{d}{dt} \dot{\mathbf{r}} = \frac{d}{dt}\left( \dot{r} \hat{\bf{r}} + r \dot{\theta} \; \hat{\boldsymbol{\theta}} \right)
\end{equation}
The new term to deal with is
$$
\frac{d \hat{\boldsymbol{\theta}}}{dt}
$$
which by similar arguments as above, we can see will be:
\begin{equation}
\frac{d \hat{\boldsymbol{\theta}}}{dt} = - \dot{\theta} \hat{\bf{r}}
\end{equation}
Add this back into our acceleration equation:
\begin{equation}
\mathbf{a} = \left( \ddot{r} \hat{\bf{r}} + \dot{r} \frac{d\hat{\bf{r}}}{dt} \right) + \left( \left( \dot{r} \dot{\theta} + r \ddot{\theta} \right) \hat{\boldsymbol{\theta}} + r \dot{\theta} \frac{d \hat{\boldsymbol{\theta}}}{dt} \right)
\end{equation}
Acceleration in polar coordinates:
\begin{equation}
\mathbf{a} = \left( \ddot{r} - r \dot{\theta}^2 \right)\hat{\bf{r}} + \left( r \ddot{\theta} + 2 \dot{r}\dot{\theta} \right)\hat{\boldsymbol{\theta}}
\end{equation}
Example
A mass $m$ is spun around in a circle of radius $R$ at angular velocity $\omega$. Using Newton's 2nd law in polar coordinates, find the tension in the string. No other forces are present.
Starting with
$$
\mathbf{a} = \left( \ddot{r} - r \dot{\theta}^2 \right)\hat{\bf{r}} + \left( r \ddot{\theta} + 2 \dot{r}\dot{\theta} \right)\hat{\boldsymbol{\theta}}
$$
We can express the two Force components as:
\begin{equation}
F_r = m \left( \ddot{r}-r\dot{\theta}^2 \right)
\end{equation}
and
\begin{equation}
F_\theta = m (r \ddot{\theta}+2 \dot{r}\dot{\theta})
\end{equation}
Things simplify since $\dot{r} = \ddot{r} = 0$, and $\ddot{\theta} = 0$
The only force acting is in the (-) radial direction, thus:
\begin{equation}
F_r = -T = -mR\omega^2
\end{equation}
This is the familiar centripetal force, $m v^2 / R$ since $\omega = v/R$