Calculus of Variations
Origins
Snell's Law
Waves at an interface
If one treats light as a wave-like phenomena, then Snell's law is readily derivable from geometry.
But, back in 1600's the nature of light (i.e. particle or wave) was anything but settled.
Principle of Least Time
Light traveling between a and b. How does it know which way to go?
Q: How does a photon (i.e. not a wave) decide to change directions upon entering and exiting the medium?
A: It has to get to point b in the shortest time.
Since the distance $s$ traveled in time $t$ at a speed $v$ is \begin{equation} v = \frac{s}{t} \end{equation} and using the fact that the speed of light depends on the local index of refraction: \begin{equation} v_\textrm{light} = \frac{c}{n(\mathbf{r})} \end{equation} we can express the time to travel an infinitesimal distance $ds$ as : \begin{equation} dt = \frac{ds}{v} = \frac{ds}{c/n(\mathbf{r})} \end{equation}
Integrating this to find the total time it takes: \begin{equation} t = \int dt = \frac{1}{c}\int n(\mathbf{r}) ds \end{equation}
Finding the path ($ds$) that minimizes the total time is essentially the Principle of Least Time, though it would take a few more hundred years to figure out how to really do this math. (and even longer to figure out why it should even be true)
Assuming the index of refraction in our material $n(\mathbf{r})$ only changes with respect to the x position, we could write: \begin{equation} t = \frac{1}{c}\int ds \; n(x) \end{equation} or, using i.47 \begin{equation} t = \frac{1}{c} \int n(x) \sqrt{dx^2 + dy^2} = \frac{1}{c} \int n \left(x \right) \sqrt{1 + \left( \frac{dy}{dx} \right)^2} dx \end{equation} which, using the shorthand for $dy/dx = y'$ (in general, a prime will mean take the derivative w.r.t whatever the explicit independent variable is), \begin{equation} t = \frac{1}{c}\int n(x) \sqrt{1+y'^2} dx \end{equation}
Lastly, the index of refraction should not be limited to just x dependent changes: $n(x,y)$ is more general. \begin{equation} t = \frac{1}{c}\int n(x,y) \sqrt{1+y'^2} dx = \int F(x,y(x),y'(x))dx \end{equation} Now, the function $F$ can be seen to depend on $x$, $y(x)$, and $y'(x)$. The techniques that follow will seek to find the path $y(x)$ that minimizes this integral.
Getting even more general, if: \begin{equation} I = \int F(x,y(x),y'(x))dx \end{equation} Can we find paths $y(x)$ that also maximize $I$? Or, even find what we'll call a stationary path, where the value of $I$ is nearly independent of small changes in the path?
Review of Mins/Max/Saddles
The Minimums and Maximums of a 1d function.
A saddle point in 1d
Functions of Two Variables
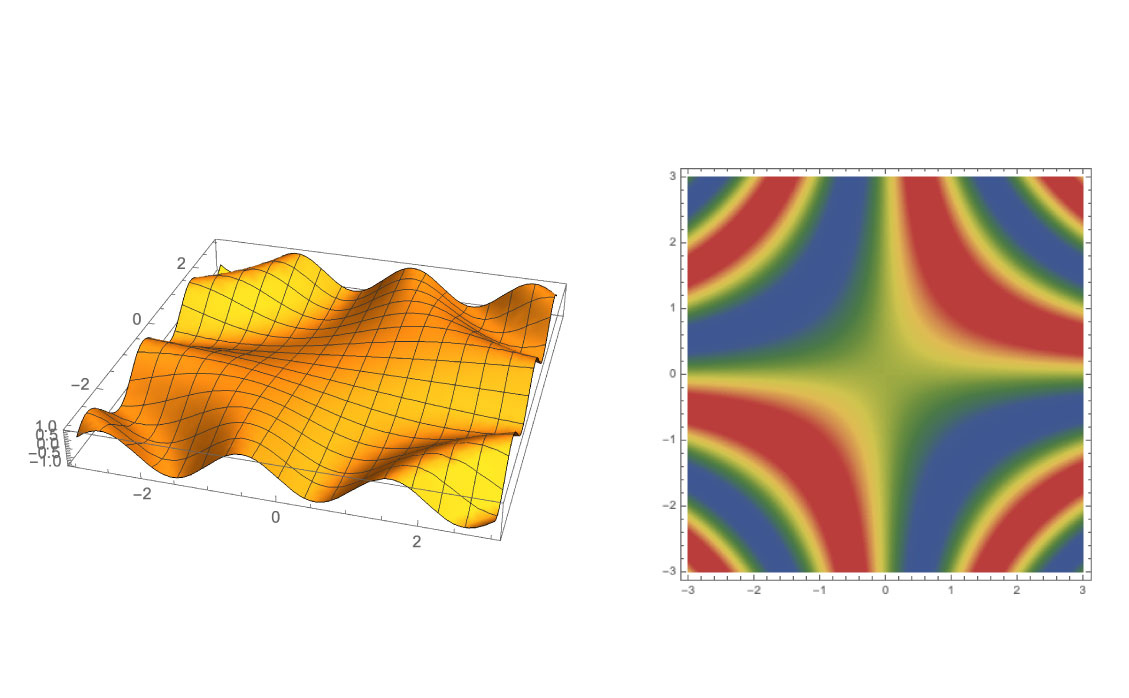
Functions of 2 variables
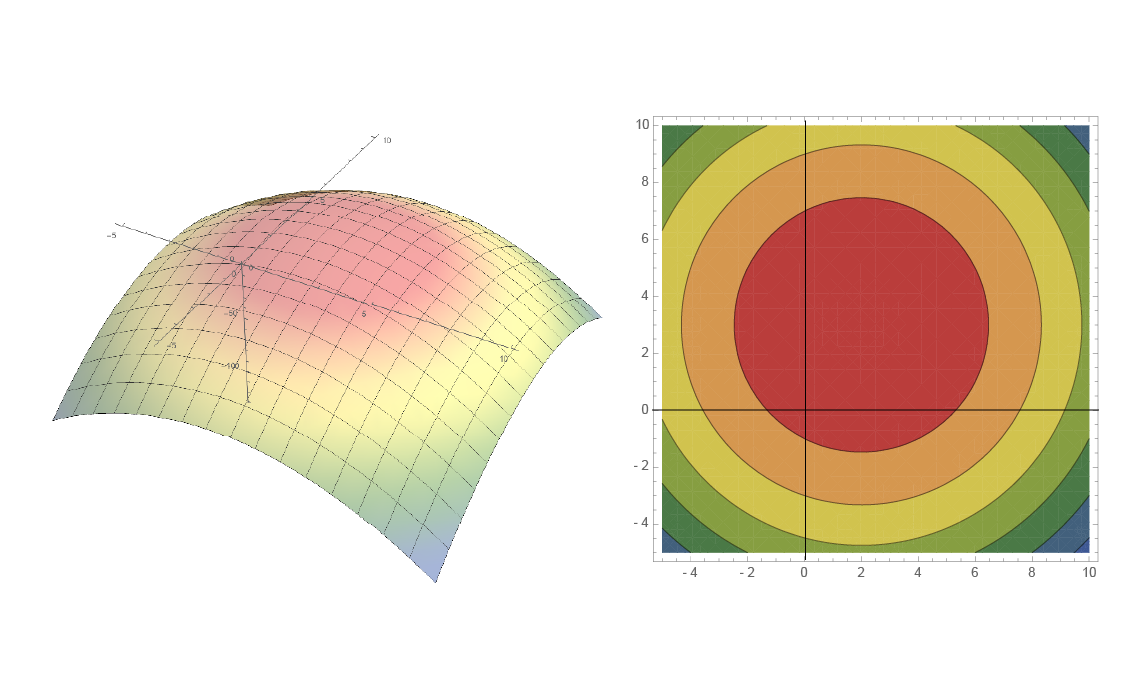
An inverted paraboloid
Find the max of this inverted paraboloid
\begin{equation} f(x,y) = -a \left( (x-x_0)^2 + (y-y_0)^2 \right) \end{equation}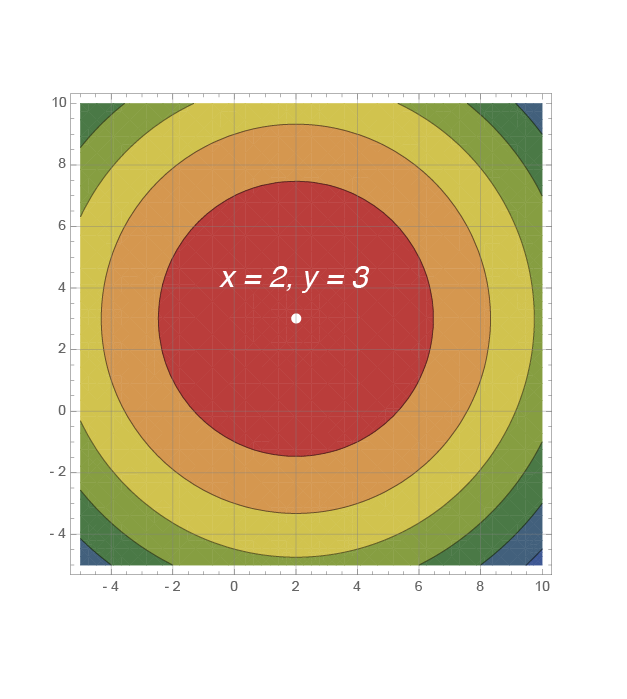
The maximum of this paraboloid
a = 1;
x0 = 2; y0 = 3;
paraboloid [x_, y_] := -a ((x - x0)^2 + (y - y0)^2)
Maximize[paraboloid[x, y], {x, y}]
Show[ContourPlot[paraboloid[x, y], {x, -5, 10}, {y, -5, 10},
Frame -> True, AxesOrigin -> {0, 0, 0},
ColorFunction -> "DarkRainbow", GridLines -> Automatic],
Graphics[{White, PointSize[Large], Point[{x, y} /. Last[%]]}]]
The path length for all the different paths from $a$ to $b$ can be considered a function.
The function is now what we want to find stationary points for.
Examples
\begin{equation} \frac{\partial F}{\partial y(x)}-\frac{d}{dx}\left(\frac{\partial F}{\partial y'(x)}\right)=0 \label{eq:eulerlagrange} \end{equation}Show that the shortest distance between 2 points is a straight line
Find the shape of a ramp that will bring a sliding mass to a lower point the fastest.
The geometry of the brachistochrone problem.
Euler-Lagrange Equation
\begin{equation} \frac{\partial F}{\partial y(x)}-\frac{d}{dx}\left(\frac{\partial F}{\partial y'(x)}\right)=0 \end{equation}The right path minimizes the integral. The wrong path does not.
Imagine a wrong curve, shown in the dotted red line.
We can call it \begin{equation} Y(x) = y(x) + \eta(x) \end{equation}
Introduce a parameter $\alpha$: \begin{equation} Y(x) = y(x) + \alpha \eta(x) \label{eq:wrongpathwithparameter} \end{equation}
Now show that \begin{equation} \frac{dI}{d\alpha} = 0 \; \textrm{for} \; \alpha = 0 \label{eq:samestartendpoints} \end{equation}
The integral $I(\alpha)$ becomes, when written out: \begin{equation} I(\alpha) = \int_{x_a}^{x_b} F(Y, Y', x) dx \end{equation} or \begin{equation} I(\alpha) = \int_{x_a}^{x_b} F(y+\alpha \eta,\; y'+\alpha \eta',\; x)\; dx \end{equation}
Now we evaluate $\frac{\partial F}{\partial \alpha}$
Thus, $dI/d\alpha$: \begin{equation} \frac{\partial I}{\partial \alpha} = \int_{x_a}^{x_b} \frac{\partial F}{\partial \alpha} dx = \int_{x_a}^{x_b} \left( \eta \frac{\partial F}{\partial y} + \eta' \frac{\partial F}{\partial y'} \right)dx= 0 \end{equation}
Integration by Parts
\begin{equation} \int_{x_a}^{x_b} \eta' \frac{\partial F}{\partial y'} dx = \left[ \frac{\partial F}{\partial y'} \eta(x)\right]_{x_a}^{x_b} - \int_{x_a}^{x_b} \frac{d}{dx} \left(\frac{\partial F}{\partial y'} \right)\eta(x) dx \label{eq:byparts} \end{equation}Fundamental Lemma of Calculus of Variations:
if \begin{equation} \int \eta(x)g(x) dx = 0 \end{equation} then it can be shown that $g(x)$ must be zero.
If $I$ is an extremum: \begin{equation} I = \int_{x_a}^{x_b} F \left[ y(x), y'(x), x \right] dx \end{equation} then \begin{equation} \frac{\partial F}{\partial y} - \frac{d}{dx} \frac{\partial F}{\partial y'} = 0 \end{equation}
How will we use this? \begin{equation} I = \int \left(\frac{1}{2}m v^2 - U \right) dt = \int \left(T - U \right) dt \end{equation} where \begin{equation} T = \frac{1}{2}mv^2 \end{equation} and (for gravity for example) \begin{equation} U = mgy \end{equation}