History of Planetary Motion

Claudius Ptolemy
Claudius Ptolemy (100 AD - 170 AD)
Why circles?

Copernicus - woodcut attributed to Christoph Murer, from Nicolas Reusner's Icones (1587)
Copernicus (1473-1543)
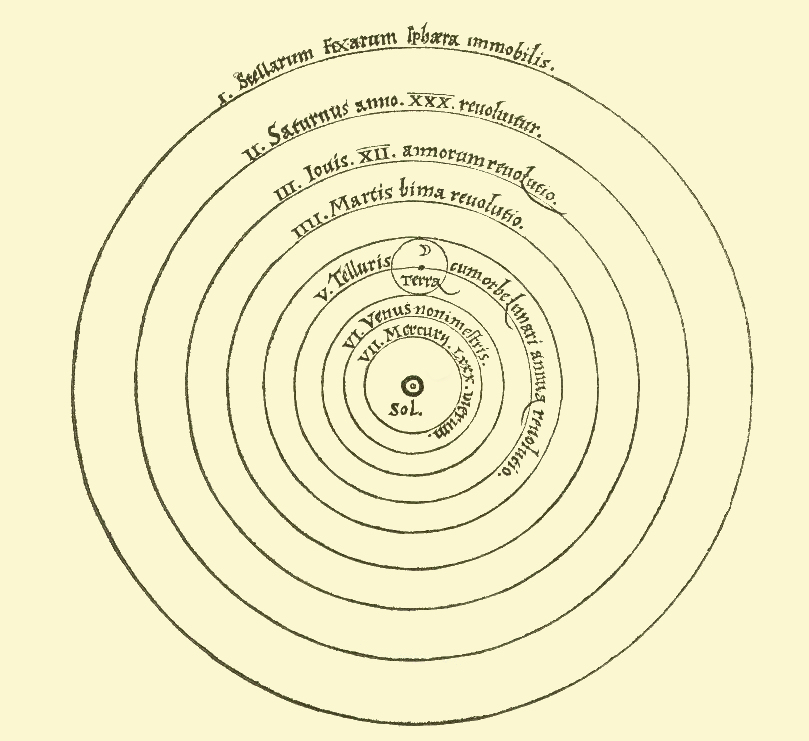
The Copernican System consisted of circular orbits centered around the sun.
Tycho Brahe

Danish astronomer Tycho Brahe [1546-1601]. Made many very good measurements of the stars and planets.
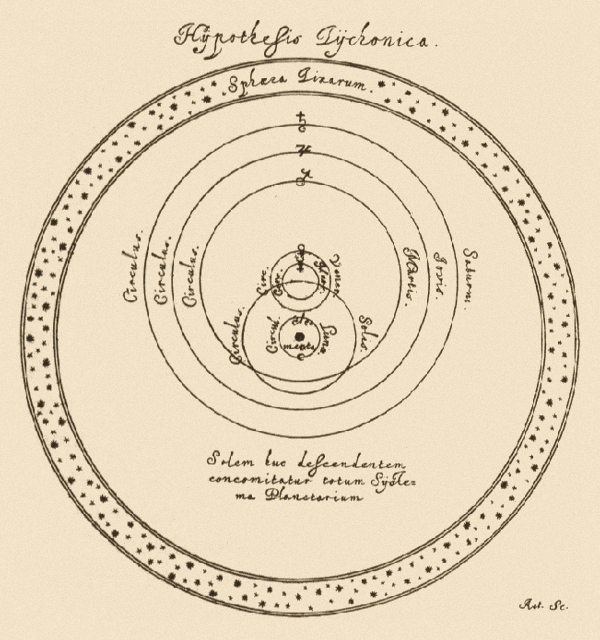
The compromise.
Johannus Kepler

German mathematician, astronomer, and astrologer. [1571-1630] Kepler was Tycho's assistant and was believed in the Copernican system.
Kepler (1571-1630)
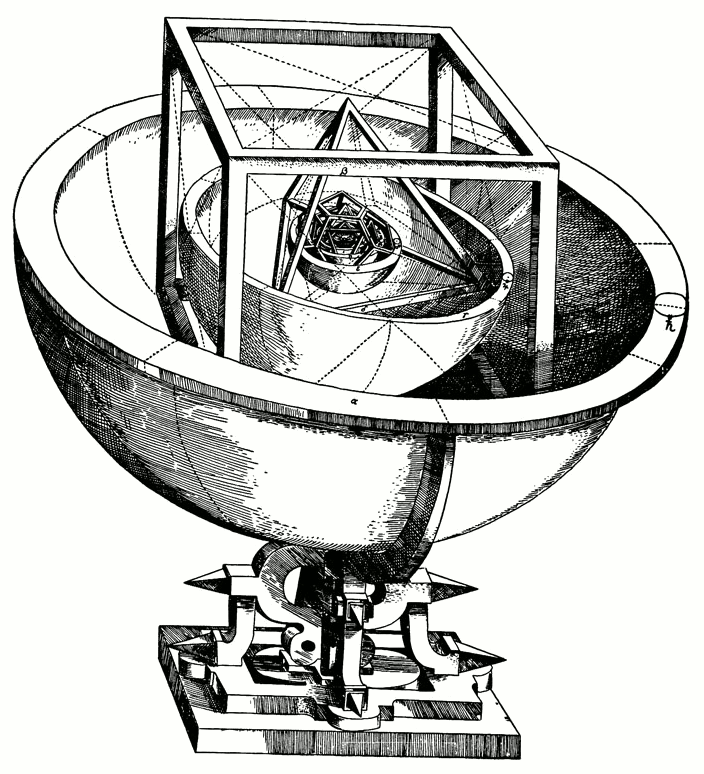
The Platonic Solid Model
Kepler's 3 laws of orbiting bodies
-
A planet orbits the sun in an ellipse. The Sun is at one focus of that ellipse.
-
A line connecting a planet to the Sun sweeps out equal areas in equal times
-
The square of a planet's orbital period is proportional to the cube of the average distance between the planet and the sun: $P^2 \propto a^3$.
1st Law: Ellipses

The orbit of Mars compared to a circle.
Mars' orbit [$e = 0.0934$] looks a lot like a circle.
2nd Law: Equal Areas in Equal Times

The blue areas in these figures will be the same if $t_2 - t_1$ is the same.

An orbiting object moves through angle $\Delta \theta$ in a given time: $\Delta t$
3rd Law
The square of a planet's orbital period is proportional to the cube of the average distance between the planet and the sun: $P^2 \propto a^3$.
\begin{equation}
t = \frac{2 \pi a^{3/2}}{\sqrt{GM}}
\end{equation}
Conic Sections
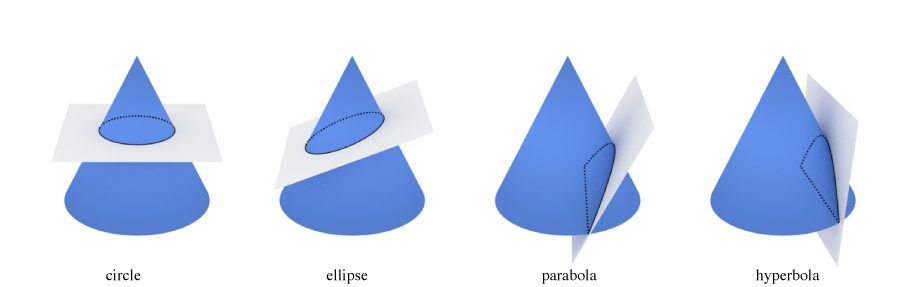
Ellipses

An ellipse satisfies this equation:
$$
\begin{equation}
r + r' = 2a
\label{eq:basic-ellipse}
\end{equation}
$$
-
$a$ is the semi-major axis
-
$r$ and $r'$ are the distances to the ellipse from the two focal points, $F$ and $F'$.
-
$e$ represents the eccentricity of the ellipse ($0 \leq e \leq 1$)
Ellipse equation in Polar Coordinates

Ellipse - the point where $r = r'$
To Show:
$$
\begin{equation}
r = \frac{a\left( 1-e^2\right)}{1+e \cos \theta}
\label{eq:polar-equation-ellipse}
\end{equation}
$$

Ellipse - and polar coordinates $r$ and $\theta$.
\begin{equation}
r = \frac{a \left(1-\epsilon^2 \right)}{1+ \epsilon \cos \theta}
\end{equation}
Characteristics of Different Orbits
Circular:
The eccentricity $\epsilon = 0$, and the radius $r$ is constant.
Both foci are located at the center.
These don't really exist in nature but are just mathematical possibilities
Elliptical

The basic parts of an elliptical orbit.
Are bound and closed orbits where the eccentricity is $0 \lt \epsilon \lt 1$
Have the gravitational center at the principle focus
$r_p = a(1 - \epsilon)$ and $r_a = a(1+ \epsilon)$
Shape is determined by any of the following pairs:
| $E$ | $l$ |
| $\epsilon$ | $r_p$ |
| $a$ | $b$ |
Parabolic
$\epsilon = 1$
Like circles, these don't actually occur but are just mathematical possibilities.
Hyperbolic
$\epsilon > 1$
Bertrand's Theorem
The only central-force potentials $U(r)$ for which all bounded orbits are closed are:
- Gravity: $U \propto \frac{1}{r}$
- Springs: $U \propto r^2$







