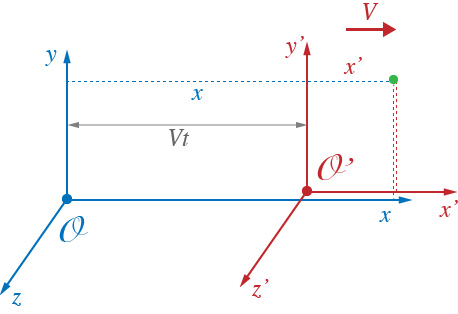
Frames of Reference
From Galileo's Dialogue Concerning the Two Chief World Systems
"Shut yourself up with some friend in the main cabin below decks on some large ship, and have with you there some flies, butterflies, and other small flying animals. Have a large bowl of water with some fish in it; hang up a bottle that empties drop by drop into a wide vessel beneath it. With the ship standing still, observe carefully how the little animals fly with equal speed to all sides of the cabin. The fish swim indifferently in all directions; the drops fall into the vessel beneath; and, in throwing something to your friend, you need throw it no more strongly in one direction than another, the distances being equal; jumping with your feet together, you pass equal spaces in every direction. When you have observed all these things carefully (though doubtless when the ship is standing still everything must happen in this way), have the ship proceed with any speed you like, so long as the motion is uniform and not fluctuating this way and that. You will discover not the least change in all the effects named, nor could you tell from any of them whether the ship was moving or standing still. In jumping, you will pass on the floor the same spaces as before, nor will you make larger jumps toward the stern than toward the prow even though the ship is moving quite rapidly, despite the fact that during the time that you are in the air the floor under you will be going in a direction opposite to your jump. In throwing something to your companion, you will need no more force to get it to him whether he is in the direction of the bow or the stern, with yourself situated opposite. The droplets will fall as before into the vessel beneath without dropping toward the stern, although while the drops are in the air the ship runs many spans. The fish in their water will swim toward the front of their bowl with no more effort than toward the back, and will go with equal ease to bait placed anywhere around the edges of the bowl. Finally the butterflies and flies will continue their flights indifferently toward every side, nor will it ever happen that they are concentrated toward the stern, as if tired out from keeping up with the course of the ship, from which they will have been separated during long intervals by keeping themselves in the air. And if smoke is made by burning some incense, it will be seen going up in the form of a little cloud, remaining still and moving no more toward one side than the other. The cause of all these correspondences of effects is the fact that the ship's motion is common to all the things contained in it, and to the air also. That is why I said you should be below decks; for if this took place above in the open air, which would not follow the course of the ship, more or less noticeable differences would be seen in some of the effects noted."
Inertial Reference Frame
A frame of reference (i.e. set of coordinates) that is not accelerating.
Any frame moving at a constant relative velocity to the original is also an inertial frame.
Galilean Transformations
Position
Velocity $\left (dx/dt \right)$
Acceleration $\left (d^2x/dt^2 \right)$
$$
\begin{align*}
x &= x' + Vt' \\
y &= y' \\
z &= z'
\end{align*}
$$
$$
\begin{align*}
v_x &= v'_x + V \\
v_y &= v'_y \\
v_z &= v'_z
\end{align*}
$$
$$
\begin{align*}
a_x &= a'_x \\
a_y &= a'_y \\
a_z &= a'_z
\end{align*}
$$
Acceleration is the same in both frames: Galilean Invariant
If you take the time derivative of position, the velocities can be obtained. The velocity in the $x$ direction differs by a constant value $V$. The second derivative of position is acceleration, and will be the same in both frames. Since the accelerations are the same in the two frames, we can call it Galilean Invariant quantity.
What about non-inertial reference frames?
These we largely ignored in Intro Physics. But, we shall ignore them no longer! Later on, we'll see cases where frames are indeed accelerating. This will come up often when looking at rotating systems.
Particles in Motion
1d Equation of Motion for Constant Acceleration
\begin{equation}
x = x_0 + v_0 t + \frac{1}{2}a t^2
\end{equation}
Where did this come from?
We can derive nearly all of kinematics (for cases with constant acceleration) by considering the relationships between derivatives and integrals. Let's begin with the definition of acceleration:
$$a = \frac{\Delta v}{\Delta t}$$
If we make the $\Delta v$ and $\Delta t$ infinitesimally small, $dv$ and $dt$, then we can rewrite this as:
$$a = \frac{d v}{dt} \Rightarrow dv = a \; dt$$
Now, we can take the indefinite integral of both sides:
$$\int dv = \int a \; dt$$
Since $a$ is assumed to be constant, we can remove from the integrand. Performing the indefinite integrals:
$$v = a t + C_1$$
where $C_1$ is the constant of integration. To determine the constant $C$, consider the equation when $t = 0$. This is the 'initial condition', thus the velocity at this point will be the initial velocity: $v_0$. We therefore obtain:
$$v = v_0 + at$$
by considering just the definition of acceleration and the concept of integration.
We can likewise consider the definition of instantaneous velocity:
$$v = \frac{dx}{dt}$$
A similar operation leads to:
$$\int dx = \int v \; dt$$
Now, we cannot remove $v$ from this integrand since it is not a constant value. However, we just figured out a relation between velocity and time above, so:
$$\int dx = \int \left( v_0 + at \right) \; dt$$
In this case, $v_0$ and $a$ are both constants. So the indefinite integral can be solved:
$$x = v_0 t + \frac{1}{2}a t^2 + C_2$$
Again, we have a constant of integration to solve for: $C_2$. Let's again consider $t = 0$, i.e. the initial condition. When $t = 0$, the object will be located at the initial $x$ position, $x_0$. Thus $C_2 = x_0$. Finally, we have an equation for $x$ as a function of time given all the initial conditions of position and velocity:
$$x = x_0 + v_0 t + \frac{1}{2}at^2$$
This is our fundamental quadratic equation that describes the motion of a particle undergoing translation with constant acceleration.
But what about when acceleration is not just a constant value?
What's the easiest $a(t)$ you can think of, where $$\frac{da}{dt} \neq 0$$
We loved that 2nd order polynomial in intro physics: $$x = x_0 + v_0 t + \frac{1}{2}at^2$$. It was great. But, those days are behind us.
Newton's Laws
In words:
No change in velocity if there is no net force acting.
A force will cause a proportional acceleration inversely proportional to the mass.
Forces come in equal and opposite pairs
In symbols:
$\Delta v = 0 $ if $F_\textrm{net} = 0$
$\mathbf{F} = m\mathbf{a}$
$F_{AB} = -F_{BA}$
These three laws will still guide much of our work in this class. We'll go well beyond the simple cases from Intro Physics though.
\begin{equation}
\mathbf{F} = m\mathbf{a}
\label{eq:newtons2ndlaw}
\end{equation}
Or perhaps as:
\begin{equation}
\mathbf{F} = m \frac{d\mathbf{v}}{dt} = \frac{d\mathbf{p}}{dt}
\label{eq:newtons2ndlawP}
\end{equation}
assuming mass doesn't change w.r.t time.
A familiar example
An object falls from a height $h$. How long does it take to hit the ground?
$$\Sigma F = F_g = ma$$
$$a = \frac{G M_E}{R_E^2} = g \approx 9.8 \; \textrm{m/s}^2$$
so, kinematics was straightforward:
$$a = \frac{dv}{dt} \rightarrow \int_{v_0}^v dv = \int_{0}^t a dt$$
What is $g$ at the height of say, the International Space Station?
Drag and Air Resistance
$$\Sigma F = F(v) + \ldots = m a$$
This leads to equations of motion that resemble:
$$ m \frac{dv}{dt} = -A v^n $$
or (ignoring the constants and stuff)
$$ \dot{v} = -v$$
($\dot{x} \equiv \frac{dx}{dt} = v$ and $\ddot{x} \equiv \frac{d^2x}{dt^2} = a$)
Air resistance was almost always ignored in introductory physics. Now, we will work on tools that will enable us to include it in the sums of forces. The key issue is that to really include the effects of drag, we'll need to add a velocity dependent force to the mix.
Easy diff. eq:
If
$$\dot{v} = b v$$
where $b$ is a constant that has units of $t^{-1}$, what is $v(t)$?
What is $x(t)$?
Since $\dot{v} = \frac{dv}{dt}$, we can rewrite that as:
$$\frac{dv}{dt} = b v $$
And now putting the $v$'s all on one side:
$$\frac{dv}{v} = b dt $$
Applying integration from suitable initial conditions:
$$\int_{v_0}^v \frac{1}{v}dv = b \int_{0}^t dt $$
yields:
$$\ln{v} - \ln{v_0} = \ln{\frac{v}{v_0}} = b t - 0 $$
or
$$v(t) = v_0 e^{b t}$$
Continuing with the same tactic to obtain $x(t)$, we have:
$$v = \frac{dx}{dt} = v_0 e^{b t}$$
Integrating again between initial and final:
$$\int_{x_0}^{x} dx = v_0 \int_{0}^{t} e^{b t} dt $$
Which will quickly come to:
$$x(t) = x_0 + \frac{v_0}{b} \left( e^{bt}-1 \right) $$
Forms of Resistance
$$f(v) = b v + c v^2 = f_\textrm{lin} + f_\textrm{quad}$$
There are several mechanisms that can cause drag . For our purposes, we can consider two:
Viscous / Stokes Drag -> Linear in velocity, $f_\textrm{lin} \propto v$
Generally dominates at low speeds
Proportional to the linear size of the object, $D$
Newtonian / Inertial Drag -> Quadratic in velocity, $f_\textrm{quad} \propto v^2$
Generally dominates at higher speeds
Proportional to the area of the object, $D^2$
Stokes Drag
\begin{equation}
F_\textrm{Stokes} = 6 \pi \eta R v
\end{equation}
$\eta$ is the viscosity of the fluid.
$R$ is the radius of the object (assumed to be a sphere)
$v$ is the velocity of the object relative to the fluid
Small particles in a fluid
Linear Drag - Bacterium
Find the $v(t)$ for a bacterium coasting in a viscous fluid. You can assume it starts with a velocity $v_0$ and then is slowed down by a force given by $F = -bv$ where $b$ is a constant that depends on the size and shape of the bacterium and the viscosity of the fluid.
Linear Drag →
$F = ma$ & $F = - b v$
Therefore, we can write:
$$ m \frac{dv}{dt} = -b v$$
or using the dot notation:
$$ m \ddot{x} = - b \dot{x}$$
Now we have an equation of motion for the bacterium. We have to now solve this to obtain the various kinematic quantities like position, velocity, and acceleration (as functions of time)
Re-arrange:
$$ m \frac{dv}{v} = - b dt $$
Now we can integrate both sides:
$$\int_{v_0}^{v} \frac{dv}{v} = -\frac{b}{m}\int_0^t dt$$
This is directly integrable and will lead to:
$$\ln {v} - \ln {v_0} = -\frac{b}{m} t$$
or using the identity $\ln{a} - \ln{b} = \ln \left( \frac{a}{b} \right)$
$$ \ln \left ( \frac{v}{v_0}\right) = - \frac{b}{m}t$$
and solving for $v(t)$
$$v(t) = v_0 e^{-\frac{b}{m} t}$$
Acceleration is just the first time derivative of velocity so we can quickly obtain:
$$a = \frac{dv}{dt} = \dot{v} = -\frac{v_0}{m/b}e^{-\frac{b}{m} t}$$
or, by defining the time constant: $\tau = m/b$
$$a = -\frac{v_0}{\tau} e^{-\frac{t}{\tau}}$$
Lastly, we need the position as a function of time as well. For that, we can integrate the velocity function since:
$$ v = \frac{dx}{dt} \Rightarrow dx = v dt \Rightarrow \int dx = \int v dt$$
In this case, $v(t)$ is straightforward to integrate so we can see that:
$$x(t) = \int_0^t v(t) dt = v_0 \int_0^t e^{-\frac{t}{\tau}} dt $$
Evaluating the definite integral then yields the following for the position:
$$x(t) = v_0 \tau \left(1 - e^{-t/\tau} \right)$$
Check: What happens when the drag force goes becomes negligible?
Newtonian Drag
\begin{equation}
F_\textrm{Newtonian} = \frac{1}{2} \rho v^2 c_d A
\end{equation}
$\rho$ is the mass density of the fluid.
$A$ is the cross sectional area of the object
$v$ is the velocity of the object relative to the fluid
$c_d$ is the drag coefficient
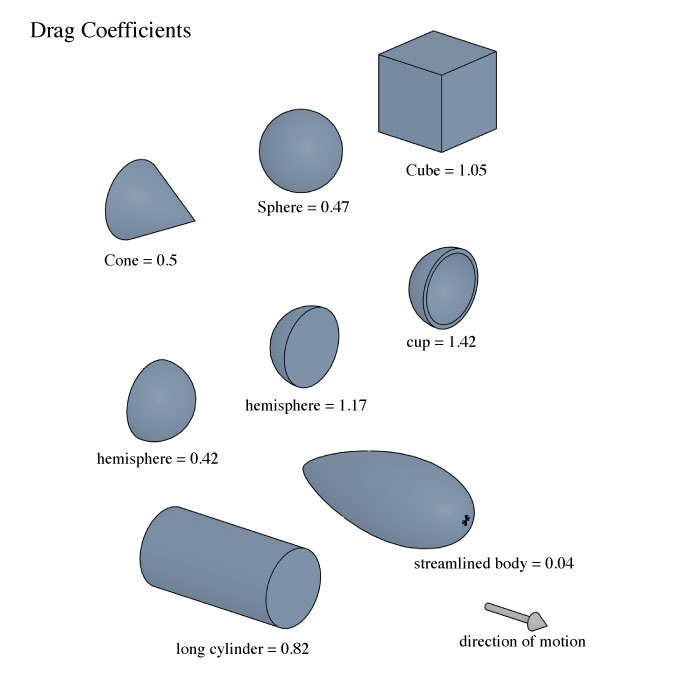
Drag Coefficients for various shapes
Reynold's number
The ratio of these two forces, the quadratic and the linear drags, can be used to describe systems:
$$\mathbf{Re}\; \textrm{or}\; R \propto \frac{f_\textrm{quad}}{f_\textrm{lin}}$$
In air...
\begin{equation}
\frac{f_\textrm{quad}}{f_\textrm{lin}} = \frac{cv^2}{bv} = \left(3.2 \times 10^{3} \frac{\textrm{s}}{\textrm{m}^2} \right) R v
\end{equation}
We can take this ratio and use it to figure out which terms are important. All the constant are given by the various parameters of air (for example) and can be merged into one number multiplied by the radius and the speed.
Eg, for a baseball with radius 3.5 cm, and a speed of 5 m/s, we would get
$\frac{f_\textrm{quad}}{f_\textrm{lin}} \approx 600 $
This would imply we can safely ignore the Stoke's drag, especially as the speed of the baseball increases.
A raindrop might be closer to 1, which means we can't ignore either one.
A tiny particle floating gently in the air might have a value in the order of $10^{-7}$, which means the quadratic drag is negligible.
History of Free Fall
What comes to mind when you see this?
This is of course the famous Leaning Tower of Pisa, a bell tower in the Italian city of Pisa (1372). It's often cited as an example for the turning point of science, when experiments became the true test of an idea. It's very likely this account is more fanciful than truthful, but it can provide an interesting investigation, especially in the context of air resistance.
Using Newton's law of gravity, we can show that the acceleration due to gravity is independent of the objects mass:
$$ m a = F = G \frac{M_E m}{R_E^2}$$
leads to:
$$a = \frac{G \frac{M_E m} {R_E^2} } {m} = G \frac{M_E}{R_E^2} \approx 9.8 \; \textrm{m/s}^2$$
Galileo's main insight was that in the absence of air resistance, the balls should fall at the same rate.
"...Having observed this I came to the conclusion that in a medium totally devoid of resistance all bodies would fall with the same speed." Source
Set up a problem that describes an object fall under the influence of gravity that experiences a linear drag force. Use that to get an expression for the terminal velocity.
Quadratic velocity dependence
Non-Linear Drag
A ball drops from a height $h$ and reaches the ground a time $t$ later. Let the ball have a mass of $m$ and a radius of $r$. What is the height of the building in terms of $t$? Air resistance is proportional the square of the velocity.
We can start by expressing the 2nd law:
\begin{equation}
m \frac{dv}{dt} = m g - c v^2
\label{eq:newtonianDrag2ndlaw}
\end{equation}
To work this out, let's remember what happens when the drag force is equal to the force of gravity: the ball will fall at a constant speed known as terminal velocity , $v_T$. Since this occurs when the net force is equal to zero:
$$ m g = c v_T^2$$
or
$$v_T = \sqrt{\frac{mg}{c}}$$
Rearranging equation \eqref{eq:newtonianDrag2ndlaw},
\begin{equation*}
m \frac{dv}{dt} = mg - cv^2 = mg \left(1- \frac{c}{mg}v^2 \right)
\end{equation*}
and replacing $\frac{mg}{c}$ with $v_T^2$:
\begin{equation*}
m \frac{dv}{dt} = mg \left(1-\frac{v^2}{v_T^2} \right)
\end{equation*}
we eventually reach something that looks like a differential equation we can tackle:
\begin{equation}
\frac{dv}{dt} = g \left(1- \frac{v^2}{v_T^2} \right)
\label{eq:newtonianDragDiffEq}
\end{equation}
What follows now is essentially the mathematical maneuver's necessary to turn \eqref{eq:newtonianDragDiffEq} into functions for $v$ and $y$ in terms time, $t$. That is, we want to be able to say, where the object is and how fast it's going at any time $t$.
We start by getting it into some integral forms:
\begin{equation}
g \int_0^t dt = \int_0^v \frac{1}{1-\frac{v^2}{v_T^2}}dv
\end{equation}
Change of variables, where $z = v/v_T$ and then $dv = v_T dz$:
\begin{equation}
\int_0^v \frac{1}{1-\frac{v^2}{v_T^2}}dv \rightarrow \int_0^z \frac{1}{1-z^2}v_T \; dz
\label{eq:newtonianDragDiffEqZSub}
\end{equation}
Since
$$
\frac{1}{1-z^2} = \frac{1}{2}\left(\frac{1}{1+z}+\frac{1}{1-z} \right)
$$
we can evaluate \eqref{eq:newtonianDragDiffEqZSub} and obtain:
$$ g t = \frac{v_T}{2} \left( \ln \left(1+z \right)- \ln \left(1-z \right) \right)$$
which can be re-written using a log identity as:
\begin{equation}
gt = \frac{v_T}{2}\ln \left( \frac{1+z}{1-z} \right)
\end{equation}
Since $z = v/v_T$, then this equation will eventually yield an expression for $v(t)$.
Eventually, after a few lines of algebra, we can arrive at:
$$\begin{equation*}
v(t) = v_T \frac{e^{gt/v_T}-e^{-gt/v_T}}{e^{gt/v_T}+e^{-gt/v_T}}
\end{equation*}$$
which can be expressed nicely using the hyperbolic tangent:
\begin{equation}
v(t) = v_T \tanh \left(\frac{gt}{v_T} \right)
\label{eq:newtonianDragvelEq}
\end{equation}
The last thing to do is integrate the velocity function in \eqref{eq:newtonianDragvelEq} to obtain the position as a function of time:
$$\int dy = \int v dt$$
\begin{equation}
y = v_T \int_0^t \tanh \left(\frac{gt}{v_T} \right) dt
\end{equation}
Letting $q = gt/v_T$ and $dq = \frac{g}{v_T}dt$ we can see that:
\begin{align*}
y &= \frac{v_T^2}{g}\int \tanh \left(q \right) dq = \frac{v_T^2}{g}\int \frac{\sinh(q)}{\cosh(q)}dq \\
&= \frac{v_T^2}{g} \ln \left(\cosh(q) \right) \\
\end{align*}
Moving back to $t$ from $q$:
\begin{equation}
y(t)= \frac{v_T^2}{g} \ln \left(\cosh \left(\frac{gt}{v_T} \right) \right)
\label{eq:newtonianDragposEq}
\end{equation}
In the end, we now have equations for velocity and position in terms of time:
\begin{align}
v(t) &= v_T \tanh \left(\frac{gt}{v_T} \right) \\
y(t) &= \frac{v_T^2}{g} \ln \left(\cosh \left(\frac{gt}{v_T} \right) \right)
\end{align}
Quadratic Drag Graphs
m = 1;
g = 9.80;
Cdrag = 0.5;
\[Rho] = 1.29;
r = 0.1;
A = \[Pi] r^2;
vterm = Sqrt[(2 m g )/(Cdrag \[Rho] A )];
yDrag[t_] := vterm^2/g Log[Cosh[(g t)/vterm]]
vDrag[t_] := vterm Tanh[(g t)/vterm]
Plot[yDrag[t], {t, 0, 10}]
Plot[vDrag[t], {t, 0, 10}]