Conservation Laws
Linear Momentum
\begin{equation} \dot{\mathbf{P}} = \mathbf{F}^\textrm{ext} \end{equation}
\begin{equation} \mathbf{P} = \sum{m_\alpha \mathbf{v}_\alpha} \end{equation}
Variable Mass Systems
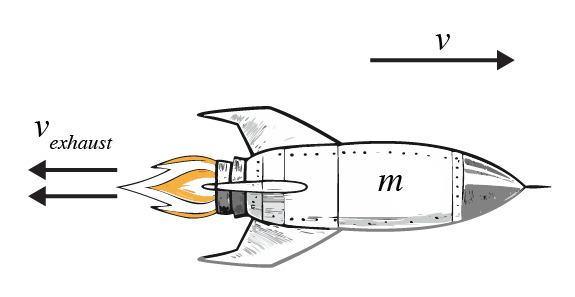
A rocket with mass $m$ moves to the right at speed $v$. The exhaust moves to the left at speed $v_{exhaust}$
\begin{equation} P(t) = mv \end{equation}
\begin{align} P(t+dt) & = (m+dm)(v+dv)-dm(v-v_{ex}) \\ & = m v + m \;dv + dm \;v_{ex} \end{align}
\begin{equation} dP = m\; dv + dm \;v_{ex} \end{equation}
If no external forces are present, then $\dot{P} = 0$ and we have \begin{equation} m \; dv = -dm \; v_{ex} \end{equation} or, after dividing by $dt$ \begin{equation} m \dot{v} = -\dot{m}v_{ex} \label{eq:rocketchangeinmomentum} \end{equation}
But, $m \dot{v}$ is just $m \;a$ so we can call the R.H.S of \eqref{eq:rocketchangeinmomentum} the thrust \begin{equation} \textrm{thrust} = -\dot{m}v_{ex} \end{equation}
Solve $$ m \; dv = -dm \; v_{ex} $$ for $v(m)$. (Initial speed and mass are $v_0$ and $m_0$ respectively.)
Angular Momentum
For a single particle:
\begin{equation} \mathbf{L} = \mathbf{r} \times \mathbf{p} \end{equation}
\begin{align} \dot{\mathbf{L}} & = \frac{d}{dt}\left( \mathbf{r} \times \mathbf{p}\right) \\ & = \left( \dot{\mathbf{r}} \times \mathbf{p}\right) + \left( \mathbf{r} \times \dot{\mathbf{p}}\right) \end{align}
but, $ \dot{\mathbf{r}} \times \mathbf{p}$ = 0 (why?) and $\dot{\mathbf{p}} = \mathbf{F}$
Thus we have the torque, $\boldsymbol{\tau}$, as the change in angular momentum \begin{equation} \dot{\mathbf{L}} = \mathbf{r} \times \mathbf{F} \equiv \boldsymbol{\tau} \end{equation}
Energy
Work & Energy
\begin{equation} T = \frac{1}{2}mv^2 \label{eq:kineticenergy} \end{equation}
How does the kinetic energy change in time?\begin{align} \frac{dT}{dt} & = \frac{1}{2}m \frac{d}{dt}(\mathbf{v} \cdot \mathbf{v})\\ & = \frac{1}{2}m \left( \dot{\mathbf{v}} \cdot \mathbf{v} + \mathbf{v} \cdot \dot{\mathbf{v}} \right) \\ & = m \dot{\mathbf{v}} \cdot \mathbf{v} \end{align}
But, $m \; \dot{\mathbf{v}}$ is the same as the force, $\mathbf{F}$ (2nd law), so: \begin{equation} \frac{dT}{dt} = \mathbf{F} \cdot \mathbf{v} \end{equation}
or, \begin{equation} dT = \mathbf{F} \cdot d\mathbf{r} \end{equation}
Using an integral formulation lets use express the change in kinetic energy for any arbitrary path: \begin{equation} \Delta T = T_2 - T_1 = \int_1^2 \mathbf{F} \cdot d \mathbf{r} \equiv W(1\rightarrow 2) \end{equation}
Conservative Forces
- Force depends only on position $\mathbf{r}$
- And is path independent
If we have a conservative force, then we can also talk about the potential energy associated with that force.
\begin{equation} U(r) = -W(\mathbf{r}_0 \rightarrow \mathbf{r}) \equiv - \int_{\mathbf{r}_0}^\mathbf{r} \mathbf{F}(\mathbf{r}) \cdot d\mathbf{r} \end{equation}
Thus we can arrive at a statement for the Conservation of Mechanical Energy, $E$. Since: \begin{equation} \Delta T = -\Delta U \end{equation} \begin{equation} \Delta \left( T + U\right) = 0 \end{equation} and then: \begin{equation} E = T + U \end{equation}
If there are non-conservative forces present, i.e. friction, then the change in mechanical energy is just the work done by the non-conservative force: \begin{equation} \Delta E = \Delta \left( T + U\right) =W_\textrm{nc} \end{equation}