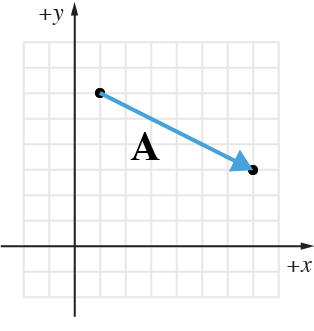
Find the two components of vector $\mathbf{A}$.
2D Kinematics
Introduction
Using + or – signs was ok in 1 dimension but is not sufficient to describe motion in 2 or more dimensions (i.e. most of the real world)
(Good thing we are now master vector operators!)
To do: Extend definitions of displacement, velocity, and acceleration.
This will be the basis of multiple types of motion in future chapters
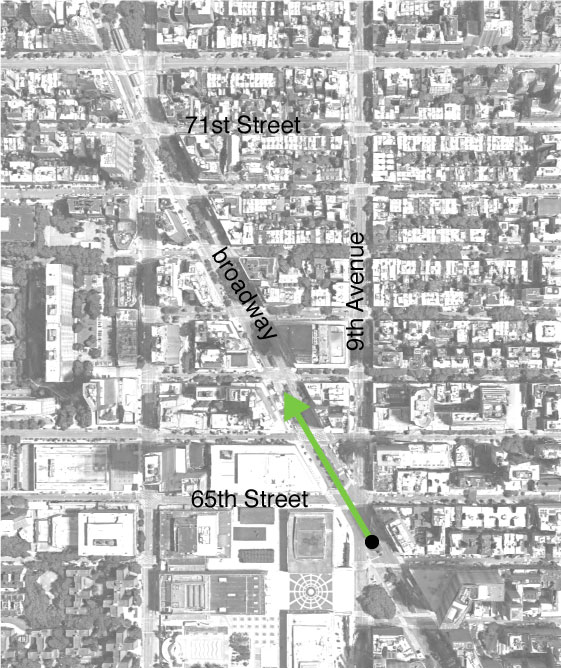
Describe the velocity vector of a bus traveling uptown on Broadway at 8 m/s. Things you know:
- It's 478 meters from 65th to 71st.
- And it's 280 meters from 9th to 10th Ave.
Vectors
In 1-D, all we needed was $\mathbf{x}$.
For 2-D motion, we'll need a displacement vector made up of two components: $$\mathbf{r} = \mathbf{r}_x + \mathbf{r}_y$$
For 3-D motion, we'll need a displacement vector made up of three components: $$\mathbf{r} = \mathbf{r}_x + \mathbf{r}_y + \mathbf{r}_z$$
Our fly starts at the position $\mathbf{r}_0$. Then he walks around until he gets to position $\mathbf{r}$.
To quantify the total displacement, we'll use the familiar formula:
$$\Delta \mathbf{r} = \mathbf{r} - \mathbf{r}_0$$We can also visualize this motion by performing the vector subtraction (addition)
$$\Delta \mathbf{r} = \mathbf{r} + (- \mathbf{r}_0)$$Now we want to imagine checking the position of Mr. Fly with a finer precision. This means we'll look for displacement vectors at short elapsed times.
Decreasing our $\Delta t$ time allows us to get a more complete picture of the motion.
Remembering average velocity as:
$$\overline{\mathbf{v}} = \frac{\Delta \mathbf{r}}{\Delta t},$$we can see how our assessment of the velocity during a given time would be better by taking smaller times to measure.
We can even get to the limit where our $\Delta t$ is very small.
$$\mathbf{v} = \lim_{\Delta t \rightarrow 0}\frac{\Delta \mathbf{r}}{\Delta t}$$This gives us the instaneous velocity.
This way, we can imagine finding the instantaneous velocity at any point in very complicated path.
The instantaneous velocity vector is directed in a line which is tangent to the motion path, and its magnitude is given by: $$\mathbf{v}=\sqrt{\mathbf{v}_x^2+\mathbf{v}_y^2}$$
The acceleration vector at a position can be considered in the same way. $$\overline{\mathbf{a}} = \frac{\mathbf{v}-\mathbf{v_0}}{t-t_0} =\frac{\Delta v}{t}$$
We can graphically subtract the velocities to see the direction of the acceleration
The instantaneous acceleration will be found by considering two very close instantaneous velocities. $$\mathbf{a} = \lim_{\Delta t \rightarrow 0}\frac{\Delta \mathbf{v}}{\Delta t}$$
The diagram shows two successive positions of a particle; it’s a segment of a full motion diagram. Which of the acceleration vectors best represents the acceleration between $\overrightarrow{v}_0$ and $\overrightarrow{v}$ ? (The speed of the particle is constant. i.e. $|\overrightarrow{v}| = |\overrightarrow{v}_0|$)

A bird drops a fish while flying. The fish falls due to gravity, but also continues moving in the horizontal direction.
How do we deal with this?
Independence of Motion
The HUGE concept for 2-D (and 3-D) motion is the following:
Motion in one axis does not interfere with or effect motion in another axis.
Independence of Motion
This implies we can analyze the motions separately, which is exactly what we'll have to do.
| Equations for x motion | Equations for y motion |
|---|---|
| $v_x = v_{0x} + a_x t$ | $v_y = v_{0y} + a_y t$ |
| $x = \frac{(v_x + v_{0x})t}{2}$ | $y = \frac{(v_y + v_{0y})t}{2}$ |
| $x = x_0 + v_{0x} t + \frac{a_x t^2}{2}$ | $y = y_0 + v_{0y} t + \frac{a_y t^2}{2}$ |
| $v_x^2 = v_{0x}^2 + 2a_x x$ | $v_y^2 = v_{0y}^2 + 2a_y y$ |
x-y motions
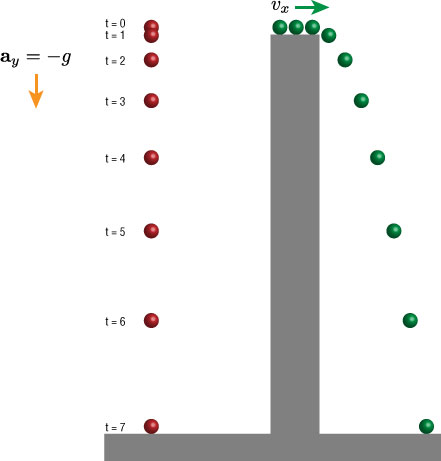
Imagine taking a series of photos at 100 ms intervals while two balls are being dropped. One is dropped straight down, the other is sent flying off in the positive x direction. The resulting image would look something like this.
Both objects have are experiencing free fall motion: they are moving under the influence of gravity only.
The green ball does have a horizontal component to its motion, but that component doesn't interfere at all with the motion in the y direction.
Projectile Motion
We assume that air resistance is negligible.
The acceleration in the y axis is constant: $$a_y = -g = -9.8 \rm m/s^2$$
There is no acceleration in the horizontal direction.
Y is positive up (+y = $\uparrow$, -y = $\downarrow$)
For an object thrown across the room, which x vs. t and y vs. t plots would you expect?
For an object thrown across the room, which x vs. t and y vs. t plots would you expect?
A stone is thrown into the air with an initial velocity of 50 m/s at 37º to the horizontal. Find (a) the total time the ball is in the air. (b) Where does the ball hit the ground? (c) What is the angle of the velocity vector when it does hit the ground?
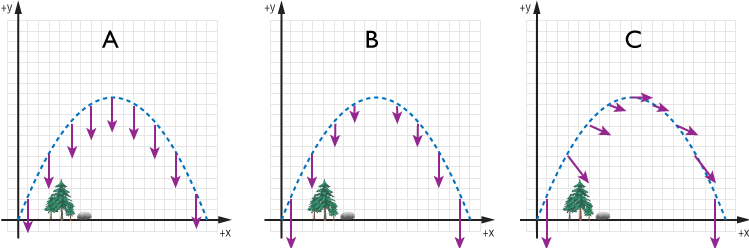
Which of the following shows the acceleration vector at various positions of an object in projectile motion
This rooftop bicyclist want to make to the next building. He’s moving at 4 m/s. The gap between buildings is 5 m. Building 1 is 20 meters high and building 2 is 12 m. Will he make it?
A ball is thrown at 60° to the horizontal. At which point(s) will the acceleration and velocity vectors $\mathbf{a}$ and $\mathbf{v}$ be parallel? (pick F is the answer is none, pick G if the answer is all points.)
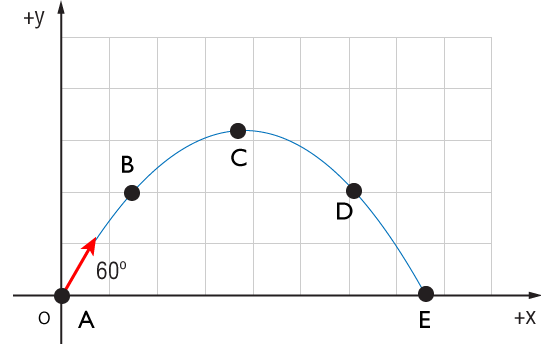
The same ball is thrown at 60° to the horizontal. At which point(s) will the acceleration and velocity vectors $\mathbf{a}$ and $\mathbf{v}$ be perpendicular? (pick F is the answer is none, pick G if the answer is all points.)

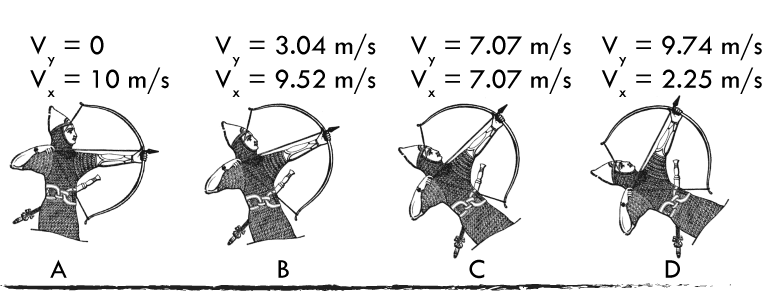
Which of these archers will shoot the arrow the farthest?
For a projectile launched from the ground with a speed $v_0$, determine the angle of launch that will give the particle the maximum distance.
Relative motion
Usually, when we speak of an object's velocity, we are considering its velocity relative to the ground. The ground becomes our reference frame. We consider it to be the stationary point of reference for all measurements of velocity.
This is not absolute however. We could imagine being inside a boat crossing the ocean. Now, the floor of the boat becomes our reference frame, which is actually moving with respect to the earth.
Here are three objects: a dragonfly, a beetle, and a rock. The rock is stationary with respect to the ground, so let's call that our frame of reference. The bug is moving and therefore has a velocity $\mathbf{v}_{B-R}$. The dragonfly is also moving with respect to the rock at a velocity: $\mathbf{v}_{D-R}$. Thus the velocity of the dragonfly relative to the beetle will be $\mathbf{v}_{D-B}$. We can see from the vectors that $$\mathbf{v}_{D-B} + \mathbf{v}_{B-R} = \mathbf{v}_{D-R}$$.
A falcon is traveling horizontally to the east at 10 m/s. It flies past a hot air balloon that is going straight up at 2 m/s. Describe the vector that indicates the velocity of the falcon with respect to the balloon.
- East and up, less than 10 m/s
- East and up, more than 10 m/s
- East and down, at exactly 10 m/s
- East and up, at exactly 10 m/s
- East and down, less than 10 m/s
- East and down, more than 10 m/s