Temperature and Heat
Two systems of temperature


Temperature conversions
C to F: multiply by 9/5 then add 32.
F to C: Subtract 32, then multiply by 5/9.
| Celsius | Fahrenheit |
|---|---|
| -30 | -22 |
| -20 | -4 |
| -10 | 14 |
| 0 | 32 |
| 10 | 50 |
| 20 | 68 |
| 30 | 86 |
| 40 | 104 |
When do the Celsius and Fahrenheit scales cross?
Real science (one scale to rule them all)
The Kelvin Scale.
The Kelvin scale is similar to the Celsius Scale in that there are 100 divisions between the ice point and the boiling point of water.
Temperature scales
| Temperature (K) | Phenom. |
|---|---|
| 0 | Absolute Zero |
| $100 \times 10^{-12}$ | Lowest Lab Temperature |
| $100 \times 10^{-3} $ | My experiments |
| $4$ | Boiling Point of Helium |
| $77$ | Boiling Point of Nitrogen |
| $293$ | Room Temperature |
| $737.5$ | Mean Temperature on Venus |
| $1670$ | Blue Candle Flames |
| $5780$ | Sun's Surface |
Effects of temperature on materials
Linear Thermal Expansion
The length, $L_0$, of a solid changes by an amount $\Delta L$ when its temperature changes by $\Delta T$.
$$\Delta L = \alpha L_0 \Delta T$$where $\alpha$ is the coefficient of linear expansion.
The coefficient $\alpha$ is good to know when designing structures or devices with more than one material.
| Material | Linear coefficient ($\alpha$) |
|---|---|
| Aluminum | $23 \times 10^{-6}$ |
| Brass | $19 \times 10^{-6}$ |
| Concrete | $12 \times 10^{-6}$ |
| Copper | $17 \times 10^{-6}$ |
| Glass | $8.5 \times 10^{-6}$ |
| Quartz (fused) | $0.50 \times 10^{-6}$ |
| Glass | $8.5 \times 10^{-6}$ |
| Iron, Steel | $12 \times 10^{-6}$ |
Examples of linear thermal expansion
 $$\Delta L = \alpha L_0 \Delta T$$
$$\Delta L = \alpha L_0 \Delta T$$


The Bimetallic strip

If two metals, like brass and steel and joined together into a thin sheet like so, then when heated, since the $\alpha$ values are different for each metal, there will be significant bending of the strip.
$\alpha_\textrm{steel} = 12 \times 10^{-6}$
$\alpha_\textrm{brass} = 19 \times 10^{-6}$
The Space Needle in Seattle is 180 meters on a 0$^\circ$ C day. How much taller is it on a hot summer day? (Take hot to mean 30$^\circ$. It's also made out of steel)
Here's a piece of material which has a positive $\alpha$ value. What will happen to $r$ as the object is heated?
- r will get bigger
- r will stay the same
- r will get smaller
Explain why it sometimes helps to open a glass jar with a very tight metal lid by running hot water of it.
| Material | Linear coefficient ($\alpha$) |
|---|---|
| Aluminum | $23 \times 10^{-6}$ |
| Brass | $19 \times 10^{-6}$ |
| Concrete | $12 \times 10^{-6}$ |
| Copper | $17 \times 10^{-6}$ |
| Quartz (fused) | $0.50 \times 10^{-6}$ |
| Glass | $8.5 \times 10^{-6}$ |
| Iron, Steel | $12 \times 10^{-6}$ |
Volume Thermal Expansions
The volume, $V_0$, of a solid changes by an amount $\Delta V$ when its temperature changes by $\Delta T$.
$$\Delta V = \beta V_0 \Delta T$$Which one of the following statements is the best explanation for the fact that metal pipes that carry water can burst during cold winter months?
- Both the metal and the water expand, but the water expands to a greater extent.
- Water contracts upon freezing while the metal expands at lower temperatures.
- The metal contracts to a greater extent than the water.
- The interior of the pipe contracts less than the outside of the pipe.
- Water expands upon freezing while the metal contracts at lower temperatures.
Heat and Energy
Energy, again
Previously, we waved away the effects of 'heat'.
We said that energy was lost due to heat, and other such things.
$$E_\textrm{mech} = PE + KE$$We could account for the lost energy, but that was about the extent of our dealings.
$$W_\textrm{nc} = E_f - E_0$$Heat: The flow of thermal energy from an object of higher temperature to an object of lower temperature.
SI unit: Joule
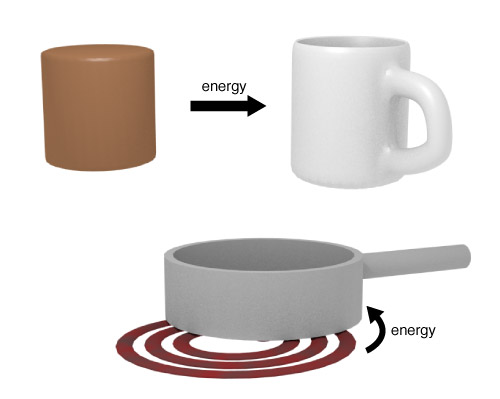
Let's say we want to change the temperature of an object by an amount $\Delta T$.
We'll need to transfer some amount of heat, $Q$, to the object in order to make this happen.
This amount will depend on the mass, $m$, of the object as well as the physical makeup of the object.
$$Q = c m \Delta T$$Here, $c$, is the Specific Heat .
Specific Heat
| Substance | c [J kg$^{-1}$ C$^{-1}$] |
|---|---|
| Solids | |
| Aluminum | $897$ |
| Copper | $387$ |
| Glass | $840$ |
| Ice | $2110$ |
| Lead | $128$ |
| Silica | $703$ |
| Liquids | |
| Ethyl Alcohol | $2450$ |
| Water | $4181$ |
The specific heat of various materials is listed here.
(all at 25ºC and 1 atm)
Compare the effects of 10000 J of heat on 1 kg of sand vs 1 kg of water.
How much heat is needed to raise a 5 kg cast-iron pot from 10 C to 90 C? What if there is also 5 kg of water in pot?
200 cm$^3$ of coffee is poured into a 150 gram glass coffee mug, which was in the cold cabinet all night and is at a temperature of 15 C. If the coffee is 95 C when it is poured into the cup, what will the final temperature of the coffee & mug system be?m
Phase Changes
Transitions
- The ice warms up from -30 to zero
- The applied heat melts the ice (0 C)
- The water is warmed from 0 C to 100 C
- The applied heat evaporates the water into steam (100 C)
- The steam is further heated
Transitions
The processes during which the ice melts is a constant temperature process.
Latent Heat
The Latent Heat of a material tells us how much heat is needed to undergo a phase transition.
For example, the Latent Heat of Vaporization, $L_V$, for water is $22.6 \times 10^5$ J/kg.
Thus, to boil away 1 kg of water (~ 1 L) we would need to apply 2 260 000 J of heat
Latent Heat of Fusion
Each type of phase transition requires its own Latent Heat Value.
The latent heat of fusion refers to the transition from a solid to a liquid.
Latent Heat of Vaporization
This value tells us how much heat is required to go from the liquid to the gas phase
The length of the plateaus in this graph are indicative of the various latent heat values.
| Substance | $L_f$ | $L_V$ |
|---|---|---|
| Water | $33.5 \times 10^4$ | $22.6 \times 10^5$ |
| Helium | x | $21 \times 10^3$ |
| Carbon Dioxide | $18.4 \times 10^4$ | $57.4 \times 10^4$ |
Eating a popsicle is hard work. How much energy is used to bring a 45 g popsicle from the freezer temperature of -10$^\circ$ to body temperature?
- c (ice) = 2090 J/(kg K)
- $L_f$ (ice) = $3.33 \times 10^5$ J/kg
- c (water) = 4190 J/(kg K)
Cooler Gas
Hotter Gas
Boiling, and vapor pressure
At the boundary between a liquid and a vapor, some of the constituent molecules will be migrating back and forth between the two phases.
In a closed container, when the same number of particles are leaving the fluid as are leaving the vapor, the vapor will be at a certain pressure. This pressure is called the equilibrium vapor pressure.
Heating the fluid will increase this vapor pressure.
The vapor pressure will be proportional to the temperature: higher temperature, higher vapor pressure.
Vapor pressure as a function of temperature.
Now we take a container open to the atmosphere.
If the vapor pressure is larger than the atmospheric pressure, then we will have unrestrained transformation from liquid to vapor i.e. boiling.
If the pressure inside a bubble is less than the pressure outside the bubble, the bubble will collapse.
If however, the pressure inside is greater than the pressure outside, then the bubble will survive!
This is boiling.
Boiling is the unrestrained conversion of the liquid to a gas (vapor). Thus, a liquid will boil when the external pressure is equal to the vapor pressure at the given temperature.
For example, we expect water to boil at 100 C, which is when the vapor pressure equals atmospheric pressure.
On a high mountain however, where the atmospheric pressure is less, then the boiling temperature is also less.

What will the temperature of the water do as I remove the air from this cylinder?
- Go up
- Go down
- Stay the same
The Transfer of Heat
Now let's ask how heat is transferred.
Essentially, there are several ways we can move this motion around.
If heat is applied to a set of molecules, their thermal motion will increase.
This means that there will be tendency to increase the volume of the space they fill.
Since density is given by $\rho = m/V $, if the volume goes up, the density will go down.
Thus, heating a material will reduce the density.
Archimedes Principle
If a region of a fluid is less dense than the rest, there will be a buoyancy force on the less dense region, and that region of less dense matter will rise compared to the other parts.
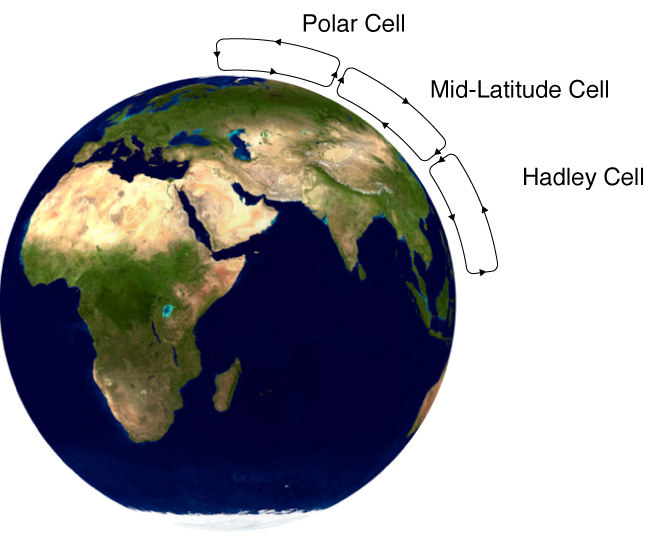
Convection
The Movement of heat via the motion of a fluid
Convection Cells
In certain situations, this flow of heat can lead to the formation of convection cells.
Here, the convection current creates a cyclical behavior in the material.
Convection Cells
Conduction
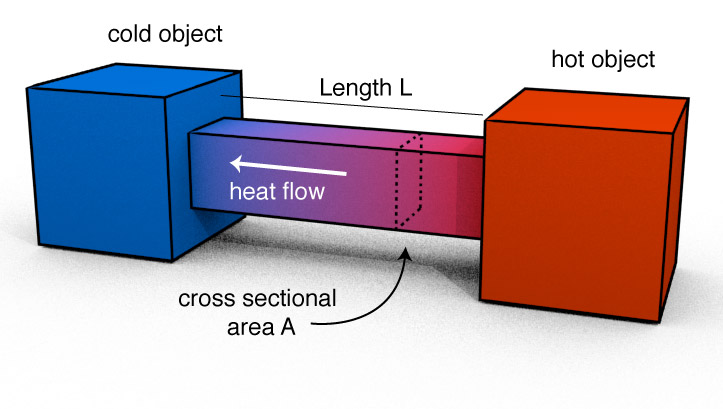
Conduction

The amount of heat we transfer should be dependent on the following:
- The Area of the connection. The larger $A$, the more heat can flow. ($Q \propto A$)
- The length of the connection. The larger $L$, the less heat will flow in a given time.
- The difference in temperature of the two objects.($Q \propto \Delta T$)
- Some constant which describes the material. ($Q \propto k$)

Indeed, we can express the amount of heat flow by the following:
$$Q = \frac{k A \Delta T t}{L}$$Some Thermal Conductivities
| Substance | Thermal Conductivity $k$ [$\rm J/(s \cdot m \cdot C^\circ)$] |
|---|---|
| Aluminum | 240 |
| Copper | 390 |
| Silver | 420 |
| Air | 0.0256 |
| Water | 0.6 |
| Wood | 0.15 |
| Styrofoam | 0.0350 |
| Vacuum | 0 |
A freezer is insulated with styrofoam. What rate must the compressor in the back of the freezer remove heat from the freezer to keep the inside at -20 C in a 25 C room? The freezer is a cube with sides of length 0.8 meters. The styrofoam is 5 cm thick and has a $k$ = 0.035.
Why are the coffee cup sleeves bumpy?
- That kind of cardboard is cheaper
- Grip is better
- That makes for a better insulator
- They are pleasing in apperance
- No reason - it was an industrial accident
Radiation
Convection and Conduction required a medium between two bodies in order for heat to flow.
However, objects can transmit energy in the form of electromagnetic waves.
The sun for example, emits EM waves and these waves transfer the energy of the sun to the earth.
There is no medium in outer space. But the waves don't need a medium...
I got a fever of 102.2 degrees F. If my mass is 70 kg, how much energy is required to make this fever happen? (I'm normally a cool 98.6 degrees)

Here is a picture of my friend Chris. He's originally from California, but now he lives in Canada. He likes a well functioning heater. Behind him is a picture of his new heater he is building with another friend Marty. It works by heating up a 550 gallon tank of water, then passing the hot water through the house. The heater has a power rating of 20 kilowatts. How long will it take to raise the temperature of the water by 33 degrees Celsius? If the power company charges 7 cents per kilowatthour, how much will it cost to heat the tank?