Fluids
(Gue)estimate the mass of the air in this room.
- 1 gram ( two raisins)
- 100 grams (an orange)
- 1 kilogram (A Chihuahua)
- 10 kilograms (A basket full of Chihuahuas)
- 100 kilograms (Two ballet dancers)
- 1000 kilograms (A small car)
- 10000 kilograms (Very large truck)
What is a fluid?
A fluid is any material that can flow.
Flow means to deform under an applied stress.
Many things can be classified as fluids: air, water, oil, syrup, etc.
Mass density
To describe these materials, we'll often use the density, $\rho$, which is defined as the mass per unit volume:
$$\rho = \frac{m}{V}$$Clearly, water will be denser than air, since 1 cubic meter of water has a much larger mass than 1 cubic meter of air.
Air: 1.29 kg/m$^3$ and water: 1000 kg/m$^3$
Estimate the mass of the air in this room
What is the volume of this cylinder?
- $4 \pi r h$
- $\pi r h$
- $3 \pi r^2 h$
- $\pi r^2 h$
- $\pi r^2 h^2$

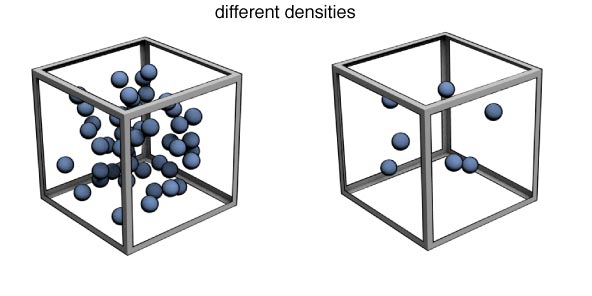
Here are two spheres. The red one has twice the radius and twice the mass of the green one. How do their densities compare?
- The Red one is four times denser
- The Red one is twice as dense
- They both have the same density
- The Green one is twice as dense
- The Green one is four times denser
A cylinder is used to hold some air that has a density of 1.5 kg per cubic meter. If the radius of the cylinder is increased by 50%, what will the density of the air be?
In a fluid, the constituent particles are continuously in motion.
Pressure
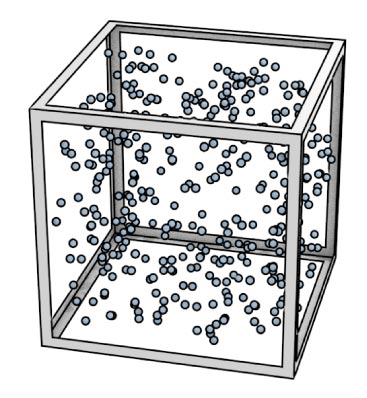
Imagine a box with 6 surfaces, each with area $A$. Inside the box are many air molecules all bouncing all over the place.
We can define the pressure, $P$, of the air in the box by considering the amount of force exerted by all these collisions on a surface of the box:
$$P = \frac{F}{A}$$If there are more collisions in a given time, then there will be a greater force, and thus a larger pressure.
Pressure
So, pressure is the force per unit area.
The SI unit is called the Pascal:
1 Newton per 1 meter$^2$ = 1 Pascal
This turns out to be not very much pressure.
We'll see that more common amounts of pressure would be several tens of thousands of Pascals: $1 \times 10^5$ Pa for example.
PSI (pounds per square inch) is also a force per area. That unit is more common in everyday life.
1 Atmosphere is another unit of pressure (atm) and is equal to 1.015 $\times 10^5$ Pa. The air molecules above are exerting that much pressure on us right now.
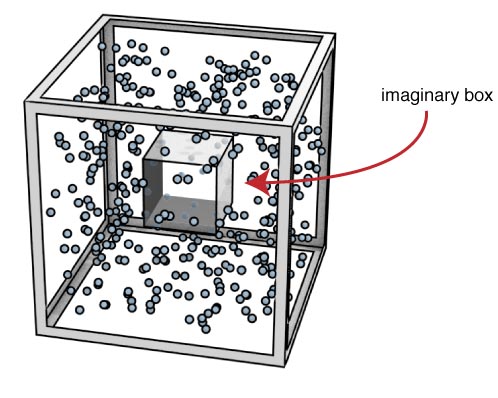
Now, we can imagine a little cube inside this space.
Each of the faces of this little cube will experience a force directed perpendicular to it.
The pressure on the little internal box will be the same as it is on the external walls.
$$P_\textrm{little box} = P_\textrm{big box}$$
because the surface areas of the box are smaller, but the number of collisions occurring on the little box is also smaller.
Now we can imagine two scenarios:
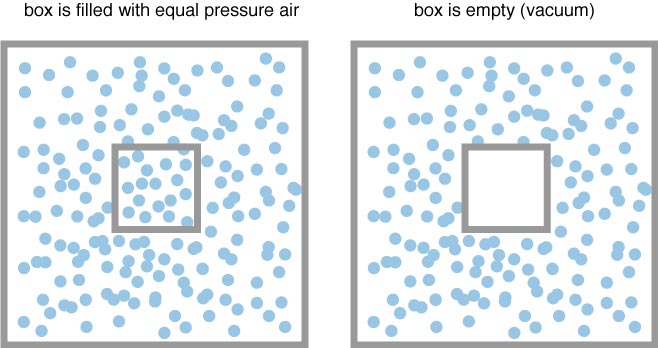
What would the forces look like on these boxes?
Compressible vs. Incompressible
In a gas, like air, the atoms have a lot of space between them. Thus, by applying a force to the container the air is in, we can compress the fluid by a significant amount.
In the case of water, the atoms are packed together about as close as possible. This makes it much harder to compress the fluid. Such a fluid is called incompressible.
Atmospheric Pressure
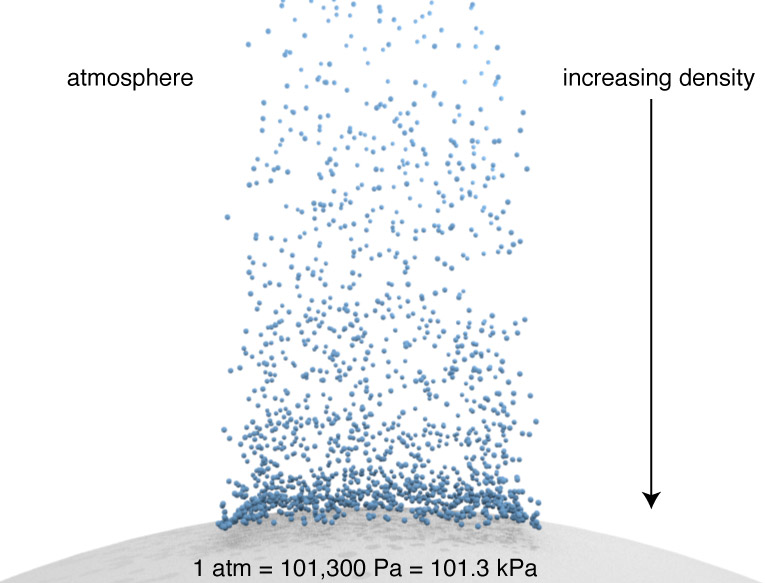
Due to gravity, the pressure close to the earth will be larger.
Pressure and depth
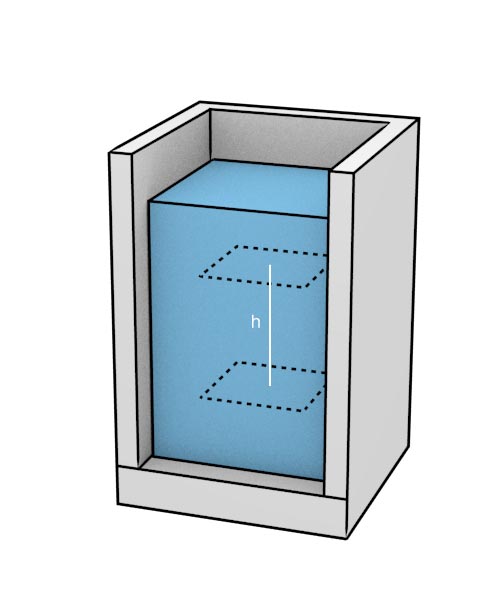
Now let's consider a column of water surrounded on all sides (4th side not shown)
What would the pressure difference be between the two dotted squares?
A free body diagram shows that:$$ \sum F_y = P_2 A - P_1 A - mg = 0$$ since the mass is not accelerating. We can use the fact that $\rho = m/(A h)$ to make this expression easier to use.
Pressure and depth
Thus, the pressure difference between two points in a vertical column of water (or other fluid) can be figured out by the following:
$$P_2 = P_1 + \rho g h$$If we know the pressure at point $P_1$, then we can use the density and the depth of the fluid below to find the pressure there.
This assumes that the $\rho$ doesn't change much with the depth. For an incompressible fluid like water, this is a good assumption.
If we are dealing with a fluid like air, then this equation would only be valid for small changes in $h$, where the density of the air did not change much.
A submarine dives to 300m. What is the pressure at this depth? (In Pa, and atm) (Density of sea water is 1030 kg/m3)
Here are two vessels connected by a tube at the bottom. If we pour water in bucket 1, how high will the water go in bucket in 2?

- bucket 2 will be at a higher level
- bucket 2 will be at the same level
- bucket 2 will be at a lower level
Here are two vessels connected by a tube at the bottom. If we pour water in bucket 1, how high will the water go in bucket in 2?
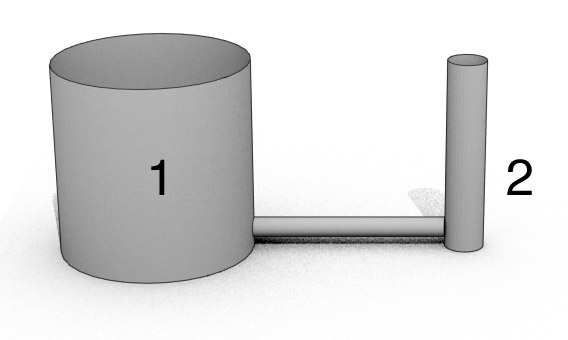
- bucket 2 will be at a higher level
- bucket 2 will be at the same level
- bucket 2 will be at a lower level
Major Consequence
In light of this relation, we can see that there is no mention of a horizontal component.
$$P_2 = P_1 + \rho g h$$This implies that the pressure along any horizontal line in a connected fluid is the same.
What is the pressure at the closed end of this tube, which is filled with water ($\rho = 1000 $kg/m$^3$)?
About how far below the surface of a lake would you have to go to have a pressure equal to twice the pressure at the top? (the density of water is 1000 kg/m$^3$ and atmospheric pressure is $1 \times 10^5 $ Pa)
- 1 meter
- 2 meters
- 10 meters
- 20 meters
- 100 meters
Pressure Gauges
The mercury barometer
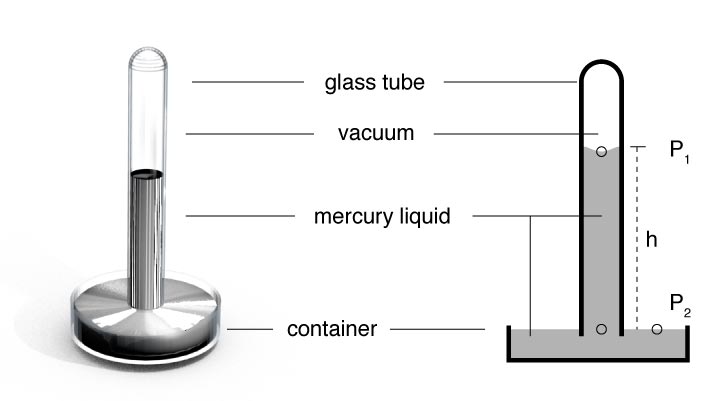
A tube, with a vacuum inside is placed upside down in a vat of mercury. The air pressure on the surrounding fluid causes the height of the Hg in the tube to rise.
Since the pressure is zero above point $P_1$, we can say $P_1= 0$. And, since the pressure is the same along any horizontal line, we can also say the pressure at points $A$ and $P_2$ are the same. Thus, we can use the depth/pressure equation to calculate the pressure at $P_2$ based on $h$, the height of the mercury in the tube.
$$P_1 = 0$$ $$P_2 = 0 + \rho g h$$And, since $P_2$ is just the atmostpheric pressure: $P_2 = P_\textrm{atm}$, we can write:
$$P_\textrm{atm} = \rho g h$$$\rho$ and $g$ are known and we can measure $h$.
Units of pressure?

The units that are reported are often a length, which is certainly not a force per unit area. (N/m 2)
But, that's ok because the density of mercury doesn't change much, and neither does $g$.
$$\rho_\textrm{Hg} = 13.6 \times 10^3 \rm kg/m^3$$ $$g = 9.8\rm m/s^2$$Thus, we can just report the units value of $h$, and eveyone around the US will probably be ok with that.
Centimeters of Hg are also sometimes used.
Manometer

A similar tool is the manometer.
The pressure at A can be determined by the height $h$. If the height $h$ is zero, then the fluid in the box is has the same pressure as the atmosphere. If not, then it will be different.
$$P_2 - P_\textrm{atm} = \rho gh$$This tells us how different the pressure is inside the box, compared to the atmospheric pressure.
When we use a drinking straw, which force causes the water to go up the straw?
- that due to a low pressure region caused by sucking
- that due to the pressure within the liquid
- that due to atmospheric pressure
- that due to the person sucking on the straw
- that due to friction forces within the straw
Pascal's Principle (or law)
"Any change in the pressure applied to a completely enclosed fluid is transmitted undiminished to all parts of the fluid and the enclosing walls."
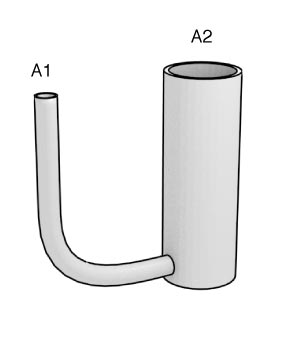
If the heights of two columns are the same, then $P_1$ has to equal $P_2$.
And since $P = F/A$, we can find the relationship:
$$F_2 = F_1 \left(\frac{A_2}{A_1} \right)$$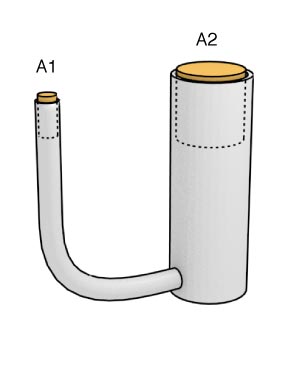
So, if we put pistons in both tubes, such that pressing on one will rise the other, we can see that based on the ratios of the areas involved, a small force on the small piston will result in a large force on the large piston.
This is the mechanism behind the hydraulic jack.
What will the scale do as I dip my finger into the water?
- The side with the water will go down
- They will stay equal
- The side with the water will go up
Bouyant Force
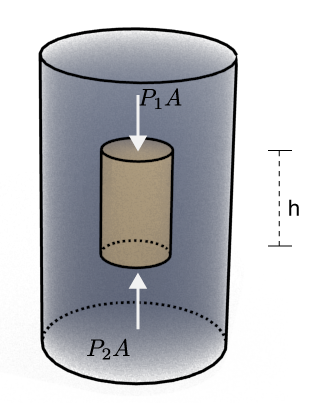
Consider a cylinder submerged in a vessel of fluid.
Since the pressure is higher at lower depths, the force on the bottom surface will be larger than the upper surface.
This difference in forces is known as the bouyant force, $F_B$.
$$F_B = P_2 A - P_1 A = (P_2 - P_1) A = \rho gh A$$Archimedes' Principle
If an object is submerged (or partially) submerged in a fluid, the magnitude of the bouyant force equals the weight of the fluid displaced.
$$F_B = W_\textrm{fluid}$$Float or sink?
Comparing the weight of the object with the Buoyant force will tell us if the object floats or sinks.
What will the scale read when I submerge the mass into the water?
- Less than 18 N
- 18 N
- More than 18 N
Does it float
Determine if this golf ball will float. (Mass = 45.33 grams, diameter = 42.67 mm)
Floating Balloons
Helium gas has a density of .166 kg/m$^3$. If the mass of an empty ballon is 2.0g, how large (i.e. its diameter) should we blow it up to achieve neutral buoyancy in air?
Holding a piece of wood underwater requires a certain amount of force. How does this force depend on the distance below the surface of the water?
- Closer to the surface will require less force.
- Deeper under the water will require less force.
- The force will be the same everywhere
The string has a mass of .46 grams per meter. How high will the balloon be able to float? The balloon has a radius of 90 millimeters and the rubber a mass of 1.5 grams. ($\rho_\textrm{He} = 0.166$ kg/m$^3$, $\rho_\textrm{air} = 1.22$ kg/m$^3$)
What happens when a certain volume of water freezes?
- It gets bigger
- It gets smaller
- It stays the same volume
What happens as water freezes?
- Its density increases
- Its density decreases
- Its density stays the same.
An ice cube is floating in a glass of water that is filled entirely to the brim. When the ice cube melts, the water level will:
- Fall
- Stay the same
- Rise, causing the water to spill
A block of wood floats in a fresh water lake. If the block of wood is 10 cm on each side, how much is sticking out above the water? (i.e. how far is it from the top of the water to the top of the wood block) ($\rho_\textrm{wood} = 700 kg/m^3$)

Which bucket, when placed on a scale, would weigh more? The water level in both is identical.
- The bucket with no oranges
- They would weigh the same
- The bucket with three oranges
- Cannot be determined
A "gold" crown weighs 8.30 Newtons. We hang the crown from a string and submerge it in water. The tension on the string is measured to be 7.81 N. Is the crown actually gold? (The density of Gold is known to be 19,300 kg/m$^3$)
Moving Fluids
Moving Fluids
Assumptions (to make things doable)
1. Steady Flow (laminar): The velocity of the fluid at any point does not change in time.
2. Incompressible: The density of the the fluid is constant.
3. Non-viscous Flow: The fluid doesn't provide any resistive forces.
Mass Flow Rate

We can figure out how much stuff is flowing through a given pipe in a time $t$.
The distance any fluid travels in a tube is given by: $\Delta x = v \Delta t$.
The volume of the fluid that passes through that length can be figured out by:
$$V = A \Delta x = A v \Delta t$$,where $A$ is the cross sectional area of the tube.
Thus, since $\rho = m/V$, the mass that flows is given by:
$$\Delta m = A \rho v \Delta t$$Mass flow rate
The amount of stuff passing through point 1 in a given time better be the same as the amount that passes through point 2.

The Continuity Equation

The mass flow rate has the same value at every position along a tube, provided the tube only has a single exit or entrance.
If the density is same (i.e. an incompressible fluid), then:
$$A_1 v_1 = A_2 v_2$$We can also talk about the volume flow rate:
$$Q = A v$$
Water pours smoothly from a faucet. Gravity causes the water to speed up as it falls. Use the continuity equation to find the volume flow rate. The two measured cross-sectional areas are: $1.2\; cm^2$ and $0.35 \; cm^2$ and they are separated by a distance of 45 mm.
A garden hose has an inner diameter of 1.6 cm. It takes 20 s to fill a 10 L bucket with it. What is the speed of the water as it leaves the end of the hose?
What about if there are changes in diameter, and elevation?
Bernoulli's Principle
For a moving fluid, what is the pressure difference between these two regions?
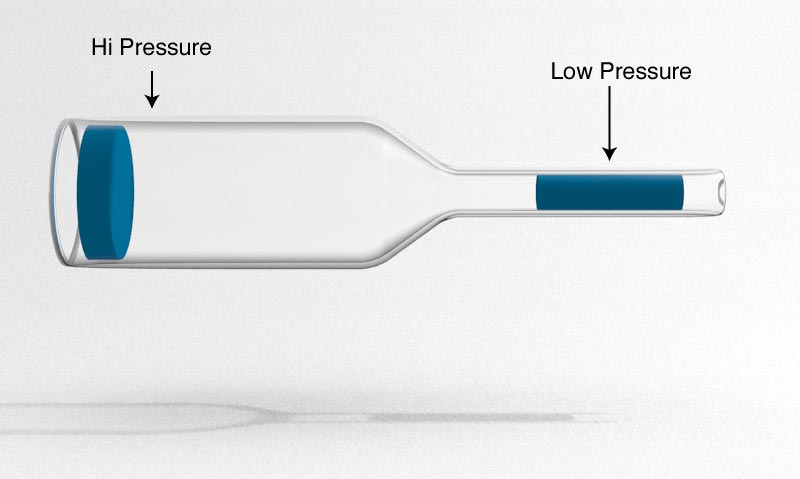
For a moving fluid, what is the pressure difference between these two regions?
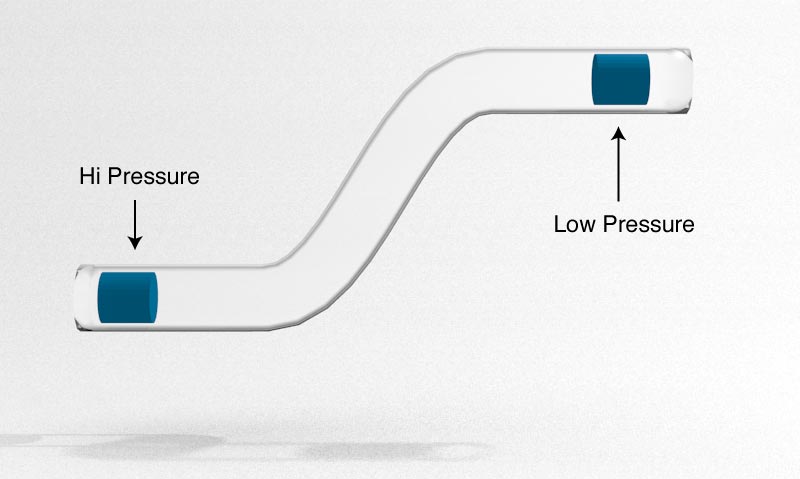
Bernoulli's Equation
$$P_1 + \frac{1}{2}\rho v_1^2 + \rho g y_1 = P_2 + \frac{1}{2} \rho v_2^2+ \rho g y_2$$This equation shows the relationship between Pressure, velocity, and elevation of a moving fluid.
If we don't worry about elevation changes, $y_1 = y_2$.
$$P_1 + \frac{1}{2}\rho v_1^2 = P_2 + \frac{1}{2} \rho v_2^2$$Applications of Bernoulli's Equation
Since the pressure above the roof can be lowered by the velocity of the wind, there will be an upward force on the roof from the high pressure air inside the house.
Fluid is flowing from left to right through the pipe shown in the drawing. Points A and B are at the same height, but the cross-sectional areas of the pipe are different at the two locations. Points B and C are at two different heights, but the cross-sectional areas of the pipe are the same at these two locations. Which of the following is true?
- $P_A > P_B > P_C$
- $P_B > P_A = P_C $
- $P_C > P_B > P_A $
- $P_B > P_A$ and $ P_B > P_C$
- $P_C > P_A$ and $ P_C > P_B$
Find the pressure at point B for this pipe full of flowing water.
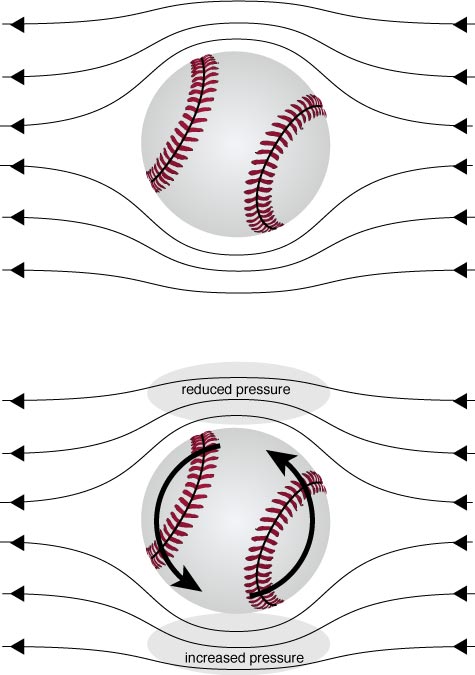
If a baseball, or any ball is thrown with out spin, then it will have the same pressure on all sides.
If however, we give the ball a large spin as it travels, the air in the immediate region of the ball will spin a little bit also. Thus, the air speed around the ball will be different on one side compared to the other.
This pressure difference will lead to forces on the ball which will cause it to venture off the straight line it would normally take.
Air flow through the tube below. What is the velocity of the air at point 1 and 2? (The liquid below is Hg, with a density of 13.6 kg/m$^3$.

A small hole opens at the bottom of a water tank. If the hole is a distance $h$ below the surface of the water, what will the velocity of the water spurting out of the tank be?