The Milky Way

Attempts to survey

Herschel

Andromeda in 1902 — Andromeda as seen in 1902.

Popular Science Monthly

The Great Debate

April 26 1920

Harlow Shapley and Heber Curtis

→ How big is the Milky Way (and the universe)

Write up: Bulletin of the National Research Council

Globular Cluster

A dense cluster of old stars.

The stars contained within are gravitationally bound to each other.

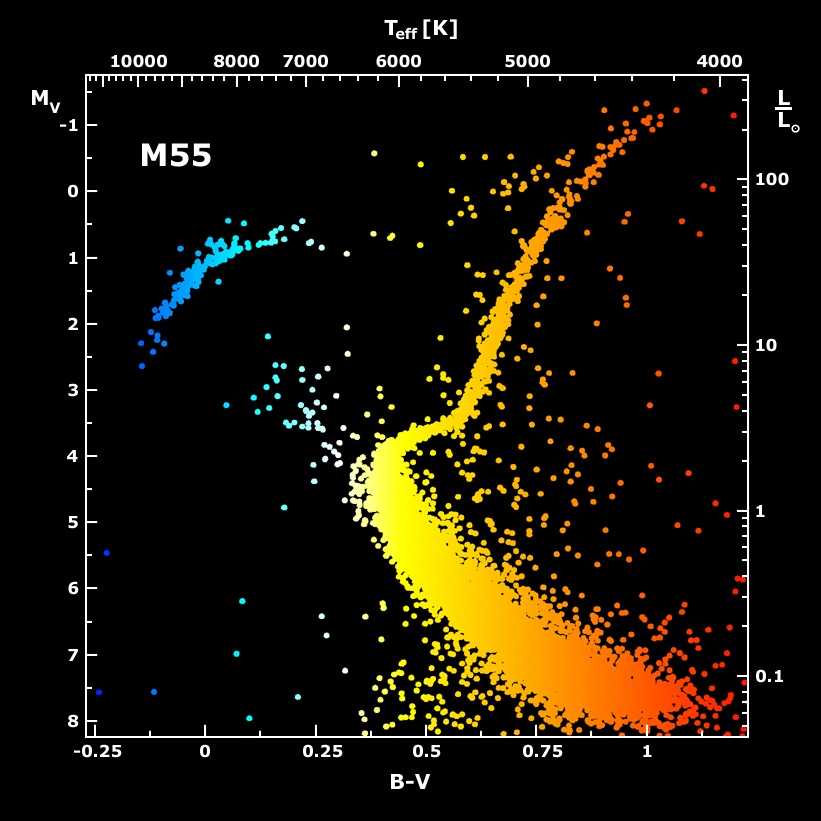
HR Diagram for a globular cluster (M-55)

https://apod.nasa.gov/apod/ap010223.html

Variable Stars

Cepheids

Brightness of some stars was found to be periodic.

cepheid-plots-2 — Ryden & Peterson Fig 17.7

Periods of 25 Variable Stars in the Small Magellanic Cloud. Leavitt, Henrietta S.; Pickering, Edward C. ; Harvard College Observatory Circular, vol. 173, pp.1-3

"A straight line can readily be drawn..."

Periods of 25 Variable Stars in the Small Magellanic Cloud. Leavitt, Henrietta S.; Pickering, Edward C. ; Harvard College Observatory Circular, vol. 173, pp.1-3

Absolute magnitude is related to period: $$\begin{equation} \bar{M}_v = -2.76 \log \left( \frac{P}{10 \; \textrm{days}}\right)-4.16 \end{equation}$$ where $\bar{M}_V$ is the absolute magnitude in the $V$ band, measured over one complete period.

With this relation, if we know $M$ and $m$, then we can get distance, $d$. $$\begin{equation} M = m - 5 \log\left(\frac{d}{10 \; \textrm{pc}} \right) \end{equation}$$

Artistic Rendering of a Pulsating Star

https://esahubble.org/videos/heic1323j/

Shapley's Map

shapley-data — Astrophysical Journal, 48, 154-181 (1918)

Known Globular Clusters in the Milky Way

Globular Clusters - more near the center.

The known Globular Clusters around our Milky Way

milky-way-our-location — image by: NASA/Adler/U. Chicago/Wesleyan/JPL-Caltech

Milky Way Structure

False-color image of the near-infrared sky as seen by the DIRBE. Data at 1.25, 2.2, and 3.5 µm wavelengths are represented respectively as blue, green and red colors. The image is presented in Galactic coordinates, with the plane of the Milky Way Galaxy horizontal across the middle and the Galactic center at the center. The dominant sources of light at these wavelengths are stars within our Galaxy. The image shows both the thin disk and central bulge populations of stars in our spiral galaxy. Our Sun, much closer to us than any other star, lies in the disk (which is why the disk appears edge-on to us) at a distance of about 28,000 light years from the center. The image is redder in directions where there is more dust between the stars absorbing starlight from distant stars. This absorption is so strong at visible wavelengths that the central part of the Milky Way cannot be seen. DIRBE data will facilitate studies of the content, energetics and large scale structure of the Galaxy, as well as the nature and distribution of dust within the Solar System. The data also will be studied for evidence of a faint, uniform infrared background, the residual radiation from the first stars and galaxies formed following the Big Bang.

Thin & Thick disks

milky-way-schematic-side — Schematic showing the main features: two disks and two spherical elements: bulge and halo.

Thin disk:

M: 6 × 10¹⁰ M☉

form: $e^{-z/h}$

$h \sim 0.350 \; \textrm{kpc}$

[Fe/H]: -0.5 to +0.3

Thick disk:

M: 0.2-0.4 × 10¹⁰ M☉

form: $e^{-z/h}$

$h \sim 1 \; \textrm{kpc}$

[Fe/H]: -2.2 to -0.5

Metallicity

The ratio of Fe to H in the spectra of stars can be used to quantify a star.

$$\begin{equation} [\textrm{Fe/H}] \equiv \log_{10} \left[ \frac{(N_{Fe}/N_{H})_{\textrm{star}}}{(N_{Fe}/N_{H})_{\textrm{sun}}} \right] \end{equation}$$

This is called the metallicity. ($N_{Fe}$ and $N_{H}$ are the number of Iron and Hydrogen atoms atoms.) Stars with the same proportion as the sun, will have values of [Fe/H] = 0. More metal rich stars have higher positive values. Less metal rich stars have negative values.

In general, younger stars will have higher metallicity than older stars.

Milky way stats

200 Billion Stars
Type: Barred spiral galaxy
Diameter: 100–180 kly (31–55 kpc)
Thickness of thin stellar disk: 2 kly (0.6 kpc)
Oldest known star ≥ 13.7 Gyr
Whole thing is moving at 600 km per second w.r.t the extragalactic frame of reference

And our place in it:

Distance to center: 26.4 ± 1.0 kly (8.09 ± 0.31 kpc)
Sun's galactic rotation period: 240 Myr

Motion of Stars

Radial velocity: $v_r$. Measured using doppler shift of the star's absorption lines.

http://spiff.rit.edu/classes/phys301/lectures/doppler/doppler.html

tangential-velocities — Ryden & Peterson, Fig 19.11

Tangential velocity: $v_t$. Measured using proper motion, $\mu$ and distance $d$. $$\begin{equation} \mu = \frac{v_t}{d} \end{equation}$$ (in the small angle limit)

http://www.backyardastronomer.com/ccd/Barnard_Mortfield_Cancelli_crop_labels1.gif

Space motion is the resultant of the radial and tangential velocities: $$\begin{equation} v = \sqrt{ v_r^2 + v_t^2} \end{equation}$$

Two stars (sun = orange, Kapteyn's Star = white)

Measuring the rotation curve

measure-distance-galactic-center — Geometry for measuring the R value for a star/cloud.

We would like to know the distance $R$. Let's say we can't measure $d$, but we know $R_0$ and $l$.

rotation-curve-and-kepler — Astrophysical Journal, Part 1 (ISSN 0004-637X), vol. 295, Aug. 15, 1985, p. 422-428, 431-436.

Dark Matter

There's more stuff there that we just can't see, so it's called dark...

Astrophycisists and Cosmology folks are still figuring out what it is.

The leading candidate is WIMPS: Weakly Interacting Massive Particle. These are hypothetical particles that don't follow the same rules as the others in the standard model of particles physics.

The Galactic Center

Can't see it too well

If we were closer...

Let's move the solar system to half a parsec away from the galactic center.

The nearest star would be ~ 1000 AU away
The night sky would have 10⁶ stars brighter than Sirius
The total starlight would be ~ 200 times brighter than the moon
Stars might collide!

sagAstar — Chandra X-ray Image of Sagittarius A*

NASA/CXC/Caltech/M.Muno et al.

Source-2-orbit — The orbits of S0-2 (black) and S0-102 (red). The data points and the best fits are shown. Both stars orbit clockwise

http://science.sciencemag.org/content/338/6103/84

Based on the orbital parameters, we can get the semi-major axis of S2: $$\begin{equation} a_{S2} = \frac{r_p}{1-e} = 1.4 \times 10^{14} \; \textrm{m} \end{equation}$$ Based on Kepler's Third law, and a period of 15.24 ± 0.36 yr: $$\begin{equation} M = \frac{4 \pi^2 a_{S2}^3}{G P^2} \\ \simeq 7 \times 10^{36} \; \textrm{kg} \\ \simeq 3.5 \times 10^{6} M_{\textrm{Sun}} \end{equation}$$

Center of Milky Way

blackhole milkyway — First image of the black hole at the centre of the Milky Way

Credit: EHT Collaboration:

Image of Black Hole at the center of the Milky Way

The Black hole at the center of the Milky Way, as imaged by the Event Horizon Telescope