Cosmology

A forest in Oregon
Olbers Paradox
If the universe is infinite, then there should be a star everywhere we look - why is it dark out?
Similarly, if we look in every direction, there should be a star there, ... eventually.
The assumptions:
- The Universe is homogenous
- The Universe is infinitely large
- The Universe is infinitely old
Distances
Many different methods for measuring distances
Radar
How long for light to travel.
Example: Lunar Laser Ranging RetroReflector (LRRR) on the moon. Measures distance to solar system objects.

Goddard's Laser Ranging Facility directing a laser (green beam)
Credit: Tom Zagwodzki/Goddard Space Flight Center

Apache Point Observatory 3.5m telescope
Credit: Apache Point Observatory 3.5m telescope running APOLLO lunar laser ranging experiment taken by Dan Long
Parallax

Bessel's heliometer
By http://www.klima-luft.de/steinicke/ngcic/persons/auwers.htm - http://www.klima-luft.de/steinicke/ngcic/persons/auwers.htm, Public Domain, https://commons.wikimedia.org/w/index.php?curid=8535990
On earth: about 100 parsecs max distance.
HST Max distance 3,000 parsecs (10,000 ly)
Gaia (10,000 parsecs with 20% error)
Milky way is at least 30,000 parsecs in diameter.
(Andromda is about 780,000 parsecs away)
Standard Candles
The flux (measured brightness) of an object depends on two things: how far away it is and its luminosity: $$\begin{equation} F = \frac{L}{4 \pi r^2} \end{equation}$$ where $L$ is the luminosity and $r$ is the distance between source and observer.
If we have a known value for $L$, then we can calculate $r$ based on the measured flux.
Some well understood physical processes can help lock in a value for $L$
Cepheids - Variable stars
Period of brightness fluctuations is related to apparent magnitude, $m$.
If we know the distance to some nearby ones (from parallax), we can calibrate the relationship.
Max: 30,000,000 parsecs (~100 million ly)
Useful for objects in this galaxy, and a few nearby ones.
Type 1A Supernova
A white dwarf in a binary system can gain mass from the companion until it reaches a limit, producing an explosion. This is a supernova. The luminosity of the resulting explosion can be predicted.
Max: 1 billion ly


SN 1054 - The Guest Star
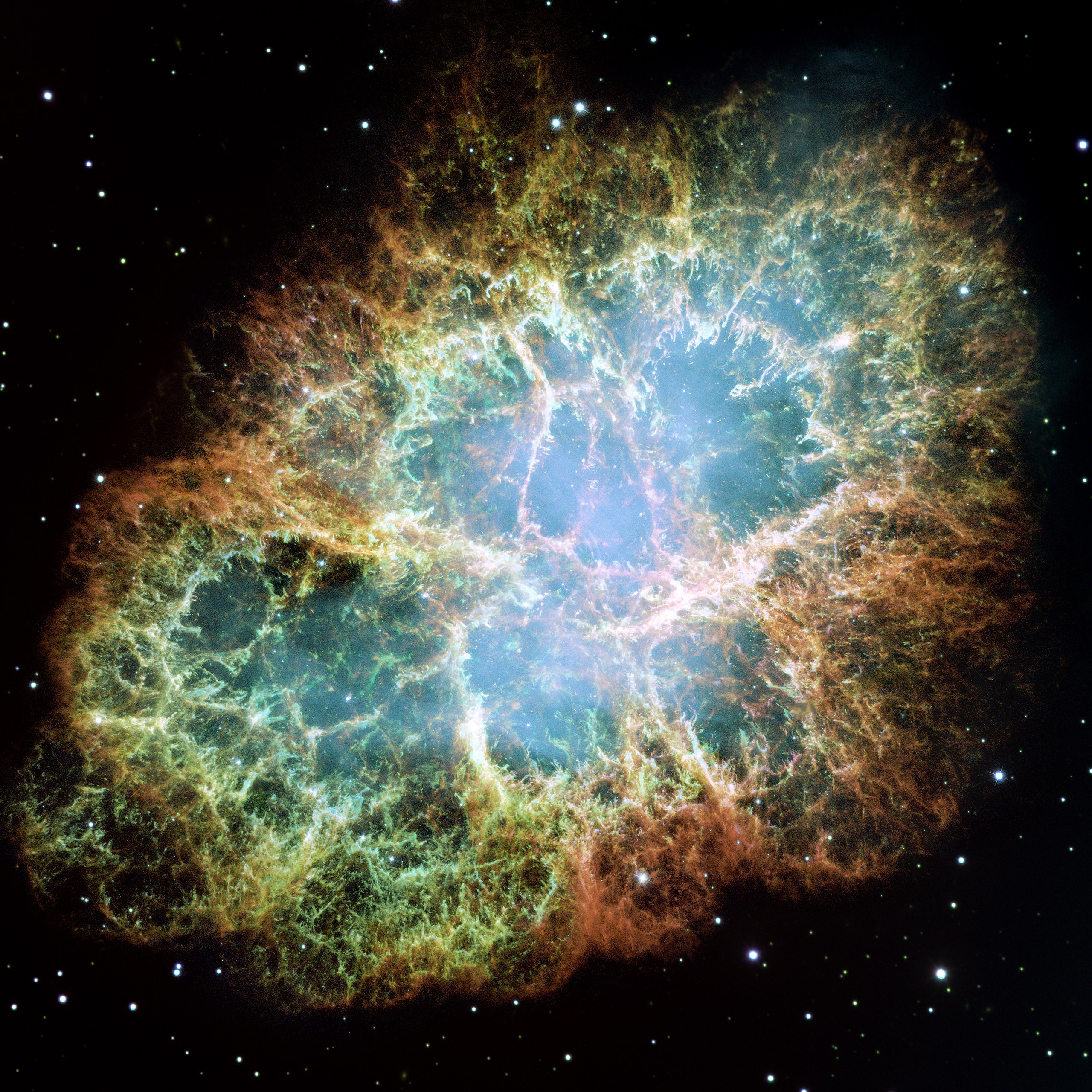
Crab Nebula, Via Hubble Space Telescope
NASA, ESA, J. Hester and A. Loll (Arizona State University)
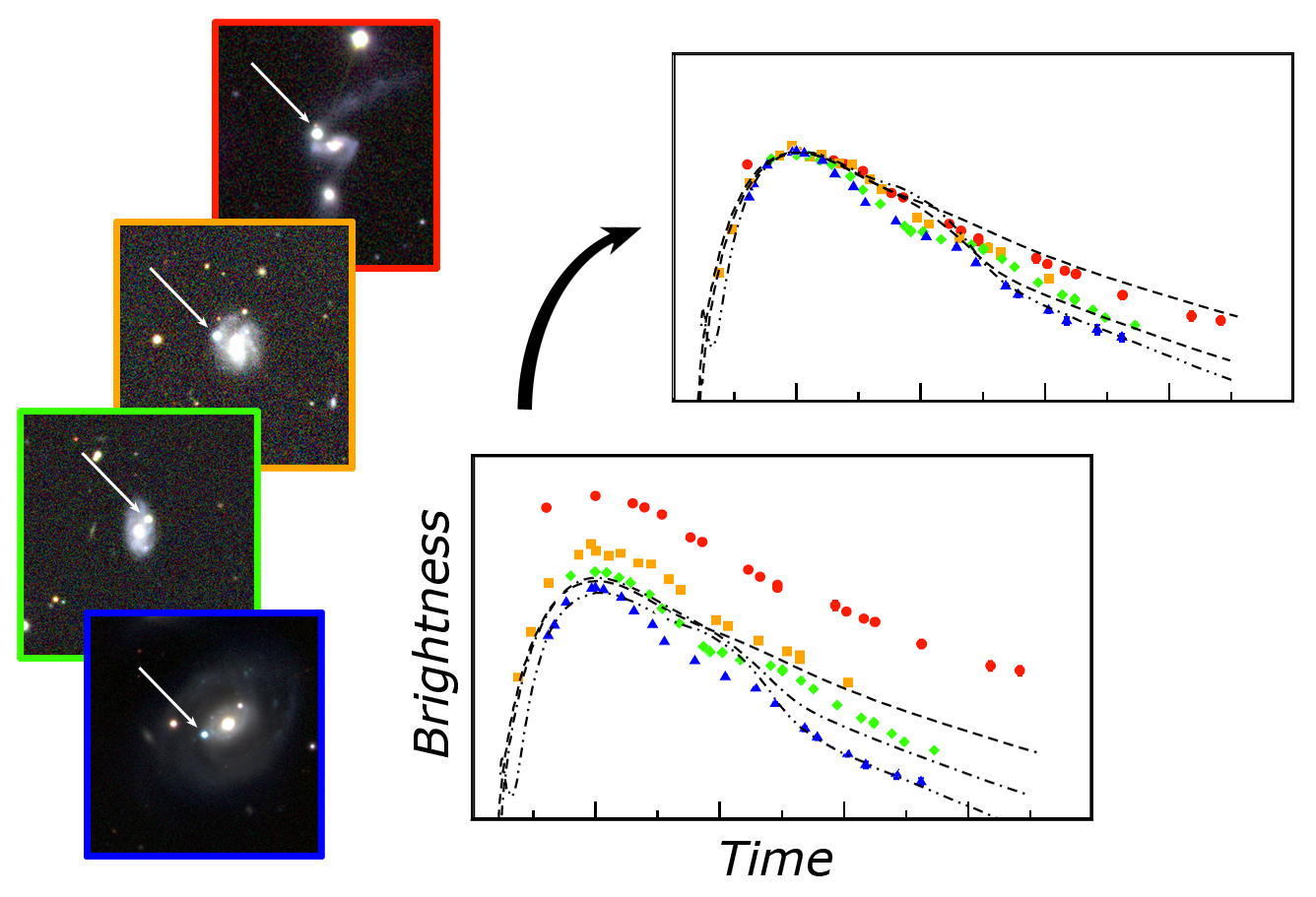
Light Curve from Supernovas
https://newscenter.lbl.gov/2014/03/03/standard-candle-supernovae/
This scientific visualization shows the development of Supernova 1987A, from the initial blast observed three decades ago to the luminous ring of material we see today.
https://hubblesite.org/contents/media/videos/939-Video

The Vera Rubin Telescope: This survey will observe the entire visible southern sky every few nights over the course of a decade, capturing about 1000 images of the sky every night and giving us a new view of our evolving Universe
https://noirlab.edu/public/images/iotw2207a/
Redshift
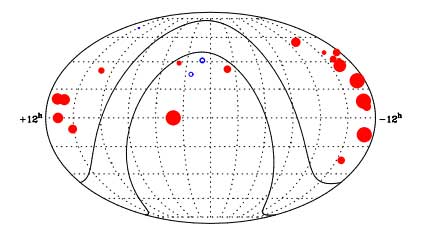
Slipher's 1917 data on galaxies apparent velocities. (nearly all are moving away from us)
Slipher, galaxies, and cosmological velocity fields, John A. Peacock
Earlier 20th century observations of galactic spectra indicated red-shifted spectral lines for most. Vesto Slipher did the first measurements of redshift in galactic spectra. This suggested they were moving away from us.

Hubble - The Realm of the Nebulae
Hubble's spectra from other galaxies.
Hubble was the first to correlate the redshifts to distance using Cepheid Variable stars outside the Milky Way.
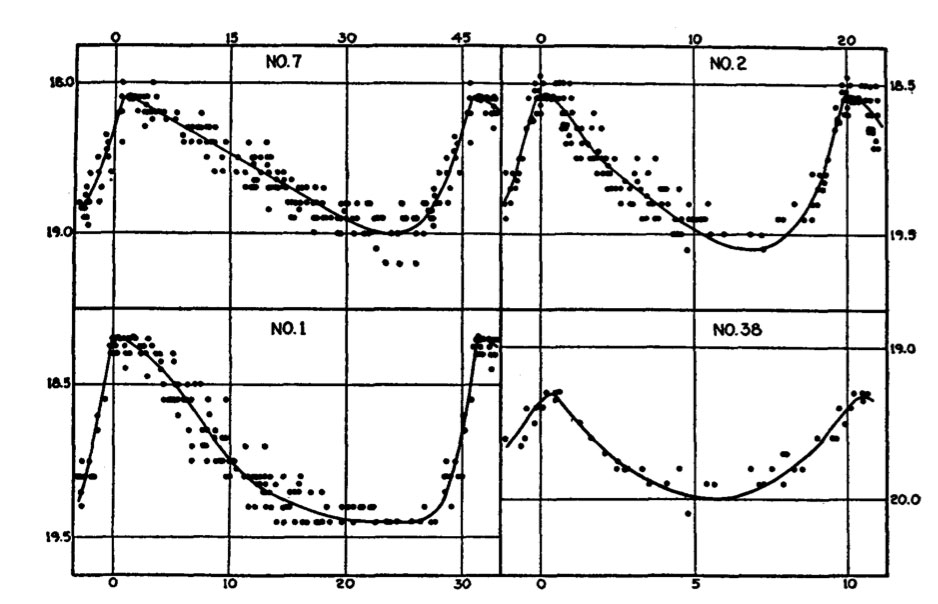
Hubble's Velocity vs. Distance curve
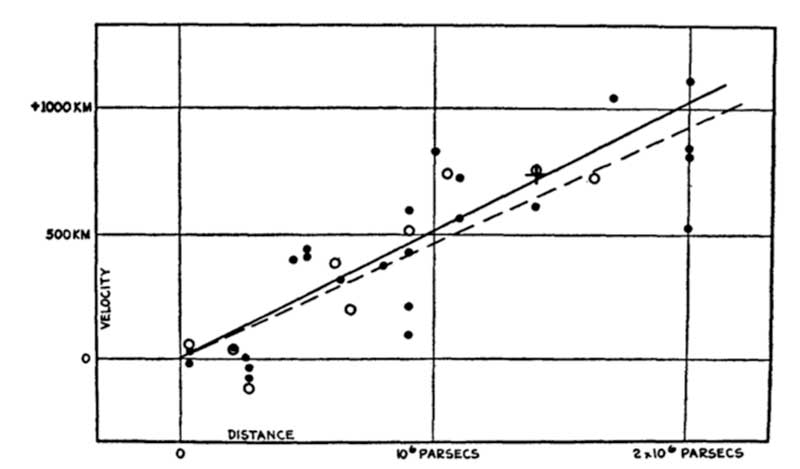
From The Realm of the Nebulae
Hubble Parameter
The Hubble parameter is just the slope of the velocity-position data:
$$\begin{equation} v = H_0 d \end{equation}$$
The value of $H$ might depend on time, so we can call the Hubble constant the value it has today: $H_0 \equiv H(t_0)$
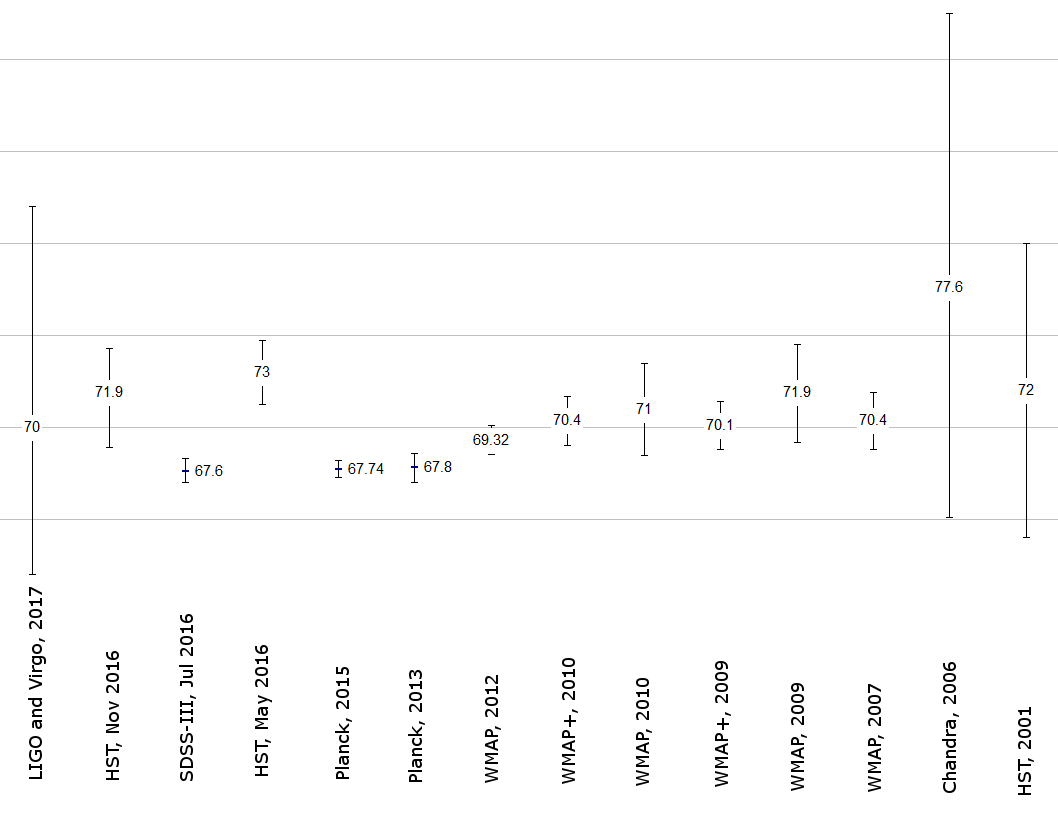
Revisions to the Hubble Constant
The current value for $H_0$ is around 70.
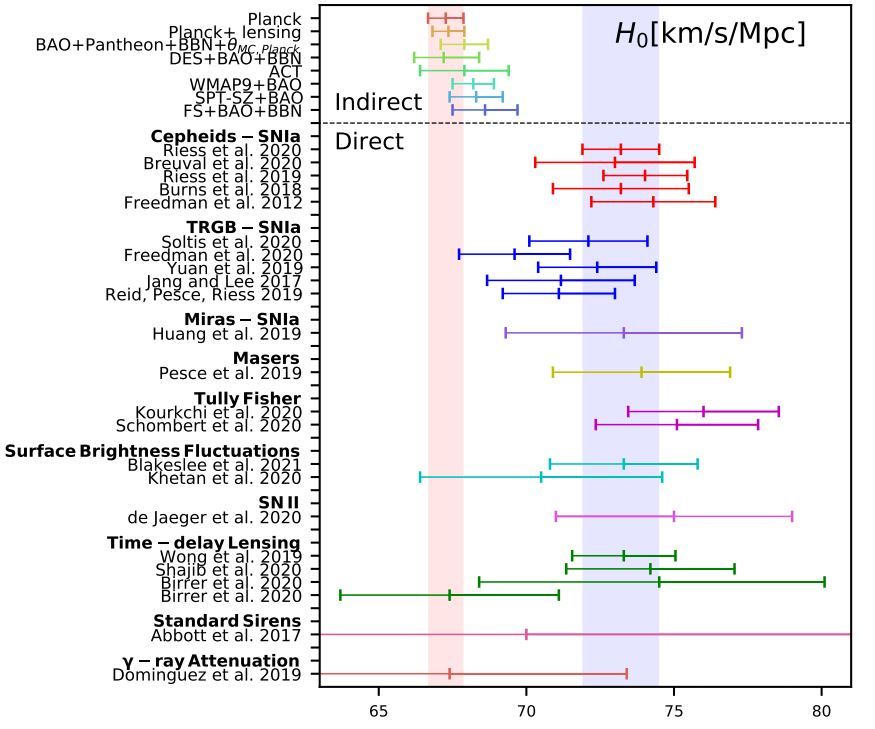
https://www.quantamagazine.org/the-webb-telescope-further-deepens-the-biggest-controversy-in-cosmology-20240813/
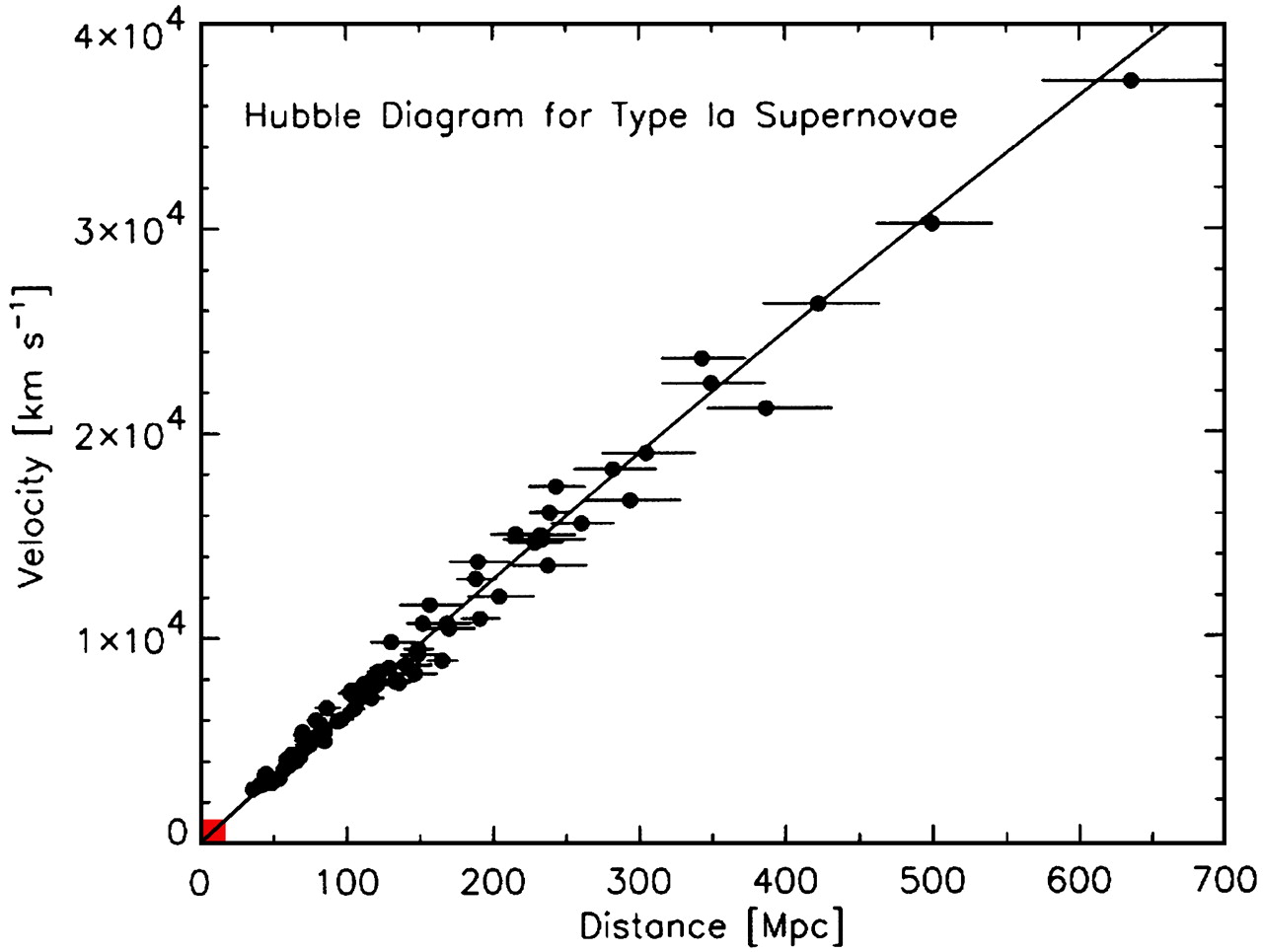
A Hubble diagram using Type 1A supernova. (Hubble's original plot is contained in the small red square in the bottom left.)
Light
Define redshift as change in wavelength w.r.t wavelength at time of emission, $e$.
$$\begin{equation} z \equiv \frac{\lambda_\textrm{0}- \lambda_\textrm{e}}{ \lambda_\textrm{e}} = \frac{\Delta \lambda}{ \lambda_\textrm{e}} \end{equation}$$
Expansion
If everything seems to moving away from everything else, then one possibility is that space is just getting bigger.
$$\begin{equation} r(t) = a(t) r_0 \end{equation}$$ where $r_0$ is the separation at the current time, and $a(t)$ is a dimensionless function known as the scale factor.
Wavelength - scale factor relation
$$\begin{equation} \frac{\lambda_e}{a(t_e)} = \frac{\lambda_0}{a(t_0)} \end{equation}$$
Thus, $$\begin{equation} 1 + z = \frac{\lambda_e}{\lambda_0} = \frac{a(t_0)}{a(t_e)} = \frac{1}{a(t_e)} \end{equation}$$
Thus, observing a quasar with $z = 6.4$ means we are looking at it when the universe was $$\begin{equation} a(t_e) = \frac{1}{7.4} = 0.135 \end{equation}$$ times smaller.
Hubble Flow
The motion of galaxies as part of the expansion is called the Hubble Flow
This can be distinguished from the peculiar velocity, which would be for example, the motion of the Milky Way towards Andromeda.
Earlier times
If we run the 'film' backwards, then earlier in time, everything would have been much closer together.
Two options: either things would be more densely packed in the beginning, or maybe there was just less stuff.
Steady State Universe
Theories were proposed that suggested the universe was non changing in fundamental appearance.
Maybe the amount of matter was changing over time, so that the average density of the universe remained constant.
Big Bang
Another option was that the density was greater earlier in the history of the universe.
Also, the universe would have to be hotter too.
Big Bang Implications
Blackbody radiation for a temperature of around 3 K.
The amount of He-3 present in the universe can be used to figure out the temperatures necessary in the very early universe. Then based on the expansions rates, we can figure out a temperature that the universe should be at now.
Rough estimates predicted 3-5 K.
If the universe were a blackbody, this should be convertible to a peak wavelength.
Cosmic Microwave Background

The Holmdel Horn Antenna that Penzias and Wilson used to first measure the CMB.
By NASA - Great Images in NASA Description, Public Domain, https://commons.wikimedia.org/w/index.php?curid=6463768
Isotropy/Anisotropy
Is it the same everywhere?
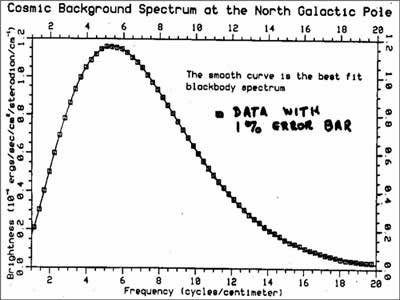
Data from the first 9 Minutes of the COBE satellites mission.
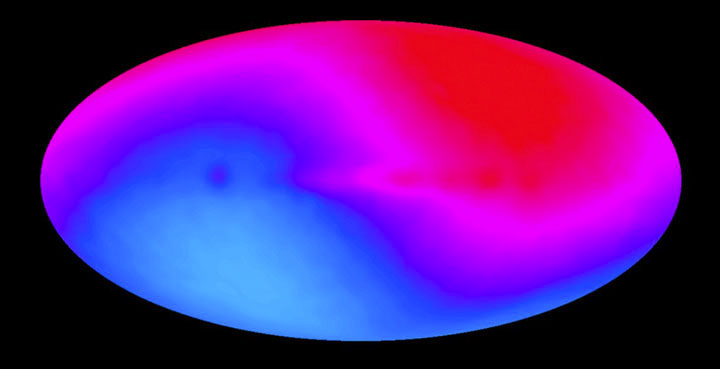
Dipole Anistropy
COBE dipole data
The CMB has a dipole anisotropy. This is likely due to the motion of the local group of galaxies compared to the rest of the visible universe, or the Hubble Flow.
How to make a CMB?
The ionized, opaque universe before recombination
- Start with a really hot dense beginning: $T \gg 10^4 \; \textrm{K}$. At these temperatures, baryonic matter will be completely ionized.
- Any photons will scatter off electrons and the universe will be opaque.
- A dense, hot, and opaque medium will produce blackbody radiation.
Transparent universe after recombination
- As the universe expands, the temperature cools. Around $T \sim 3000 \; \textrm{K}$, the protons and free electrons combine to form neutral atoms.
- Now, the blackbody photons are free to stream throughout the universe.
Cooling of the CMB
The energy density of a photon gas: $$\begin{equation} u = \left(\frac{4 \sigma}{c} \right)T^4 \end{equation}$$ and the pressure: $$\begin{equation} P = \frac{u}{3} \end{equation}$$
From the first law of thermodynamics. $$\begin{equation} dQ = dE + PdV \end{equation}$$
Since the universe is homogeneous and isotropic, we expect there to be no heat flow: $dQ = 0$.
Thus, we get: $$\begin{equation} \frac{dE}{dt} = - P(t)\frac{dV}{dt} \end{equation}$$
Substituting $u$ and $P$ from above, and taking derivatives, and simplifying: $$\begin{equation} \frac{1}{T}\frac{dT}{dt} = - \frac{1}{3V}\frac{dV}{dt} \end{equation}$$ since the volume of the universe is proportional to the scale factor cubed: $$\begin{equation} V(t) \propto a(t)^3 \end{equation}$$ we can write: $$\begin{equation} \frac{1}{T}\frac{dT}{dt} = - \frac{1}{a}\frac{da}{dt} \end{equation}$$ which can be reexpressed as: $$\begin{equation} \frac{d}{dt}(\ln T) = - \frac{d}{dt}(\ln a) \end{equation}$$ which implies: $$\begin{equation} T(t) \propto a(t)^{-1} \end{equation}$$
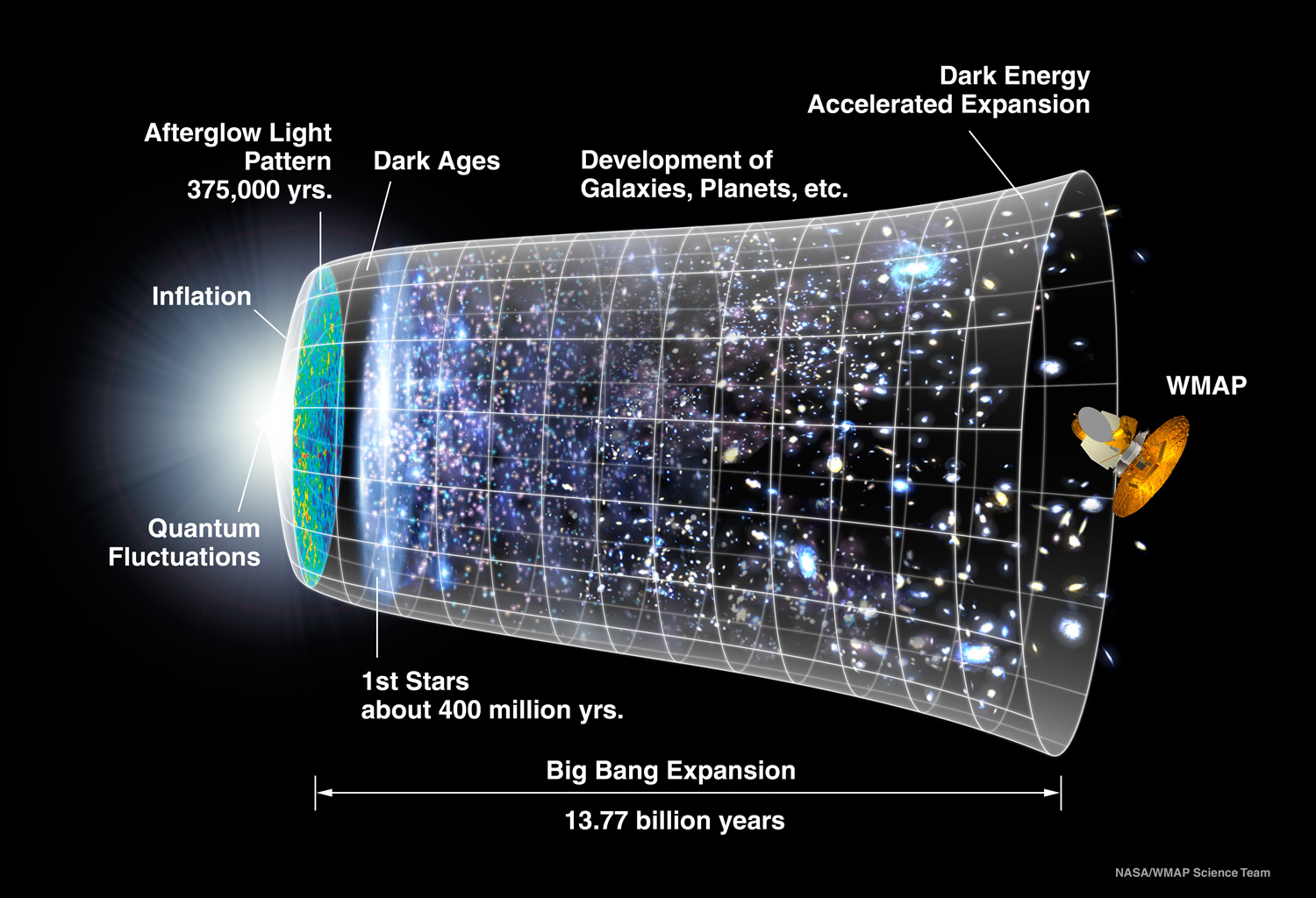
Olber's Paradox Resolution
The universe is not infinitely old.
Can't say how big it is, but only what we can see. (visible universe)