Torque
Introduction
Torque will be used to quantify forces applied to bodies which can rotate.
Previously, in the particle model, it didn’t matter where on a body we applied a force. However, with rigid bodies, that is no longer true.
(Things are no longer point particles.)

Torque
- The magnitude of the force
- The distance r, from the pivot point to where the force is applied
- The angle at which the force is applied


$F_\perp $ contributes to rotating the wrench
$F_\parallel$ does not contribute to the rotation at all.
We know from experience that
- it’s easier to open a door when you push at the point that’s farthest from the hinges
- you have to push in the direction you want it to go.
(let’s turn that into math)

Torque, $\tau$ will be given by:
$$\tau = r F_\perp$$

Lever arm changes
As the angle of the line of action changes, then the length of the 'lever arm' changes.



$$\tau = F \mathcal{\ell}$$
In general...

Either way you set it up, the torque is still given by the force applied, times the distance away from the pivot point, and the sine of the angle between the force and the radius of motion.
$$\tau = r F_\perp = r F \sin \phi$$or,
$$\tau = F \mathcal{\ell} = F r \sin \phi$$Which force will provide the largest magnitude of torque on the wrench? (E if torque is the same for each.)

Net Torques
Just like the net force, we can add up all the different torques applied to an object to see if, and which way, it will rotate.
$$\sum \tau = \tau_1 + \tau_2 + \tau_3 \ldots$$
What is the net torque around the labeled axis?
Torque
Torque, like force, is a vector
 $$\bbox[10px ,border:3px solid red]{\tau = |r||F|\sin\phi}$$
$$\bbox[10px ,border:3px solid red]{\tau = \mathbf{r} \times \mathbf{F}}$$
$$\bbox[10px ,border:3px solid red]{\tau = |r||F|\sin\phi}$$
$$\bbox[10px ,border:3px solid red]{\tau = \mathbf{r} \times \mathbf{F}}$$

To open the door, which direction should the torque vector point?
- $\mathbf{x}$
- $-\mathbf{x}$
- $\mathbf{y}$
- $-\mathbf{y}$
- $\mathbf{z}$
- $-\mathbf{z}$

What is the torque applied to the nut?
Fulcrums and Levers
Let's balance a board on a fulcrum.



A meter stick of mass 0.6 kg sits on a fulcrum located at the 30 cm mark at equilibrium. At the end of the stick (0.0 cm) hangs a mass m. What is m?
Moment of Rotational Inertia
We saw before that a force caused a linear acceleration, with Newton’s 2 ndlaw:
$$F = ma$$Since a torque is basically the rotational equivalent of force, then it should cause an angular acceleration.
$$\tau \rightarrow \alpha$$However, we need a constant of proportionality between the two terms.
$I$ is called the 'moment of inertia'.
It will describe how easy or hard it is to rotate a rigid body. (just like mass told us how hard or easy it was to move a body)
In the case of F, and linear motion, if we applied the same force to two different masses, then the heavier mass would have a smaller acceleration.
Equilibrium
Why things fall...
Equilibrium
If the following two conditions are met for any object: $$\Sigma F_x = 0 \;,\; \Sigma F_y = 0 \;,\; \Sigma F_z = 0 $$ and $$\Sigma \tau = 0$$ Then the object will be in equilibrium.
Center of Mass
There is a special point in a system or object, called the center of mass, (CM) that moves as if all of the mass of the system is concentrated at that point
The system will move as if an external force were applied to the total mass M located at the center of mass.
For a simple case, like two equal masses on a stick, our intuition should tell us that the center of mass is just in the center of the rod.

But, intuition is not enough sometimes...

Center of mass of a system like the following will be given by:

$$x_{cm} = \frac{m_1 x_1 + m_2 x_2}{m_1+m_2}$$
There are 3 object located on the x axis: Their masses are 1,2, and 3 kg and positions are x = 1m, 2m, and 3m, respectively. Draw this system and locate the center of mass
When does an object tip over?
If the center of mass is not directly over the axis of rotation, then there will be a torque on the object: $\sin(\phi)\neq0$.
Stable vs. Unstable Equilibrium
An object is in stable static equilibrium when, after a small disturbance, it returns to a state of equilibrium. A marble in the bottom of a bowl is in stable static equilibrium. A marble on the top of a dome, if balanced just right, might be in unstable static equilibrium.
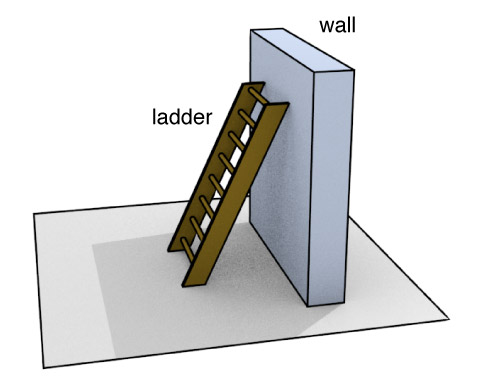
Which drawing below shows the forces that will prevent the ladder from slipping?
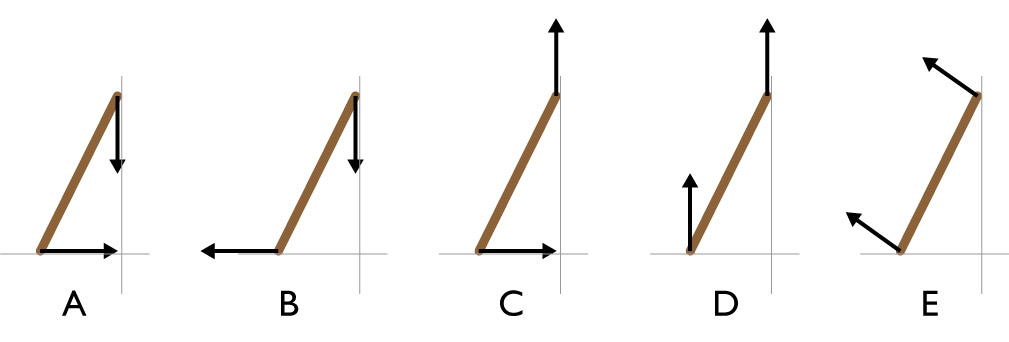
An 80 kg construction worker is sitting 2.0 m from the end of a 1450 kg steel beam to think about the state of the world. The Beam is attached to the wall with a hinge, so it can rotate. The cable supporting the beam can break if the force on it is greater than 15,000 N. Should the worker be worried?
Elasticity
Bonds within solids can be thought of as little springs.
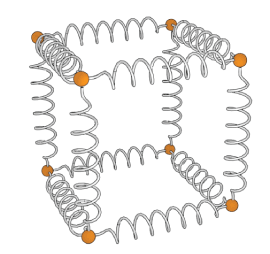
The nature of these 'springs' helps determine a given material's physical properties.
Materials
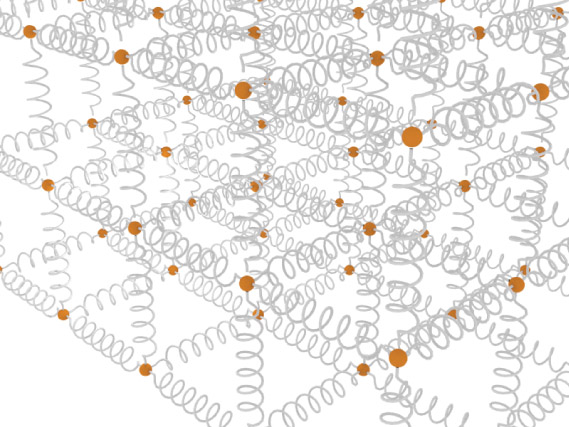
Of course, with many atoms, we'll have many springs.
This will be hard to calculate even for just a few atoms.
$$\Sigma F = \textrm{many springs}^\textrm{a very large number}$$So, we'll need a model.
Stress ∧ Strain
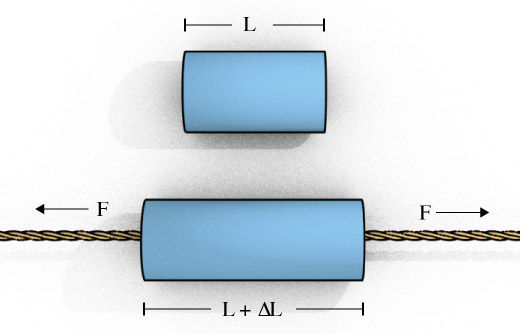
If we apply a stress to an object, there will be a resulting strain.
$$\textrm{stress} = \textrm{constant} \times \textrm{strain}$$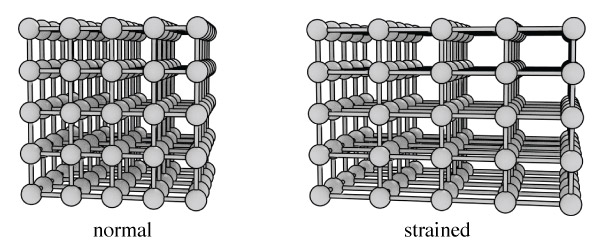
In the case of a simple, lenear deformation, this will be called a tensile strain.
Shear
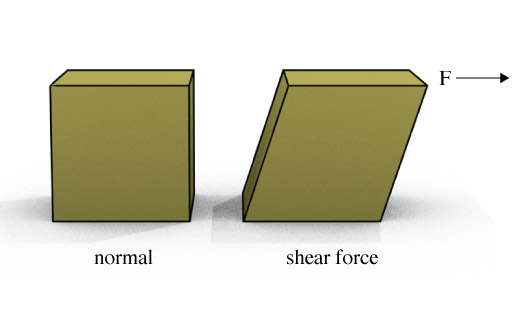
A shear force will deform an object as shown. This would be an example of shear stress.
Modulus
All of these deformations of materials can be analytically treated by using using the proper modulus.
For example, with a tensile or compressive stress, we can use Young's Modulus $(E)$ to correlate the change in length of an object to an applied force: (The force $F$ applied over a given area, $A$ is what matters)
$$\frac{F}{A} = E \frac{\Delta L}{L}$$| Material | Young's Modulus (GN/m$^2$) |
|---|---|
| Diamond | 1,220 |
| Steel (A36) | 200 |
| Aluminum | 69 |
| Oak Wood | 11 |
| Teflon | .5 |
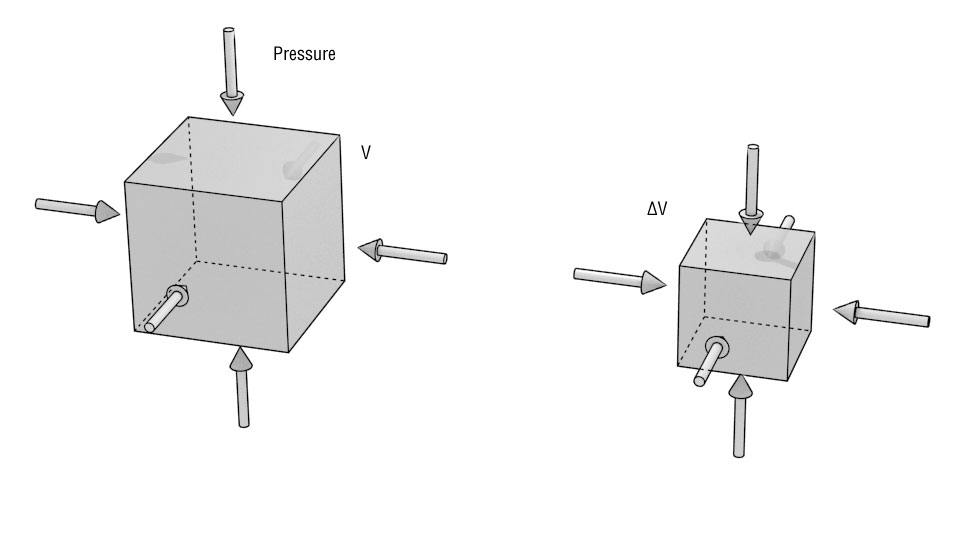
Volume Compression
If an object is compressed on all sides (like when it's underwater), then the volume of the material can change. This is dealt with by considering the bulk modulus, $B$.
$$p = B \frac{\Delta V}{V}$$Here, $p$ is pressure. So, for example, water has a bulk modulus of $2.2 \times 10^9$ N/m$^2$. It will deform ever so slightly under pressure.