Explaining Nature Without Words
Visualizations in Physics and Science from Ancient Times to Virtual RealityAn overview
- Some generalizations about people and the world that I have little supporting evidence for, but seem legit.
- A brief history of science visualization
- Science sims at CCNY
- The future
Nature
Nature is messy.



Organizers


Prediction
Why? So we can predict the future.
Science
Sharing

Mode of Communication



Language

Math
The book of nature is written in the language of mathematics.
- Galileo
Visual Communications
What we learn merely through the ear makes less impression upon our minds than what is presented to the trustworthy eye.
- Horace, ca. 20 BC

Eidos in Greek became idea
Imagination -> image
Visual Thinking
Examples from Ancient Times

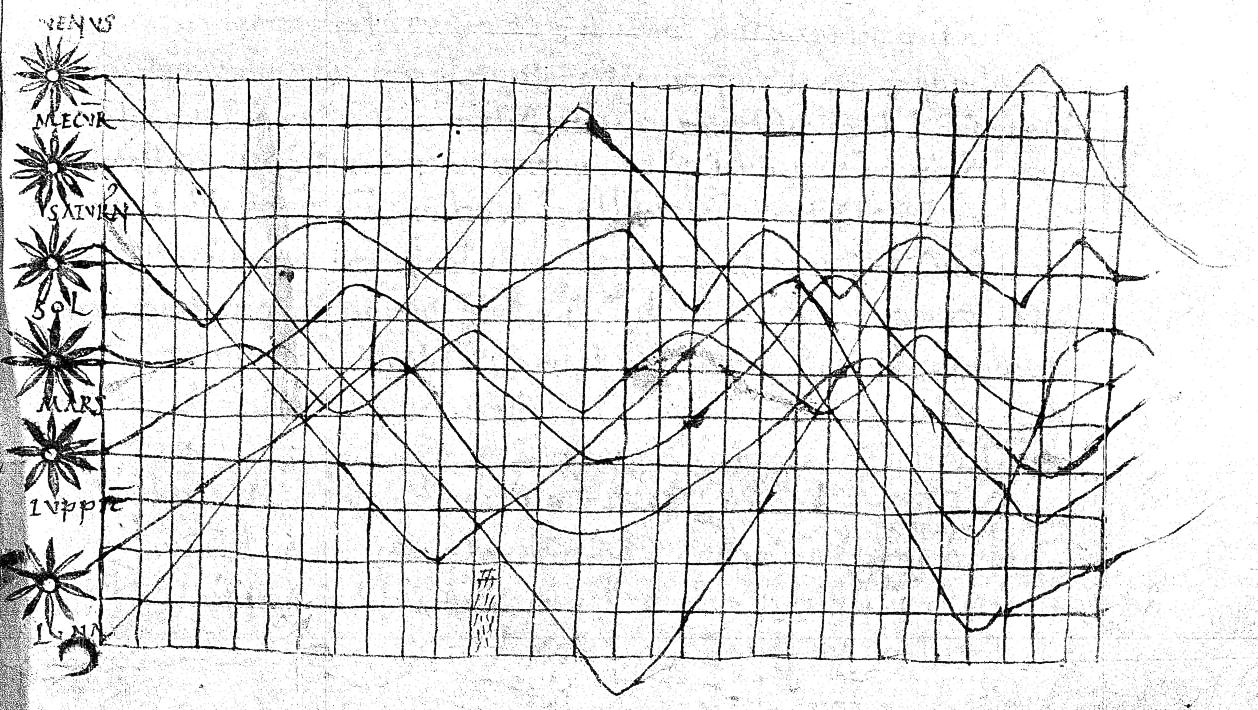
A Babylonian Tablet
c. 1900-1700 BC
Other Geometrical Figures



Nicole Oresme
Descartes
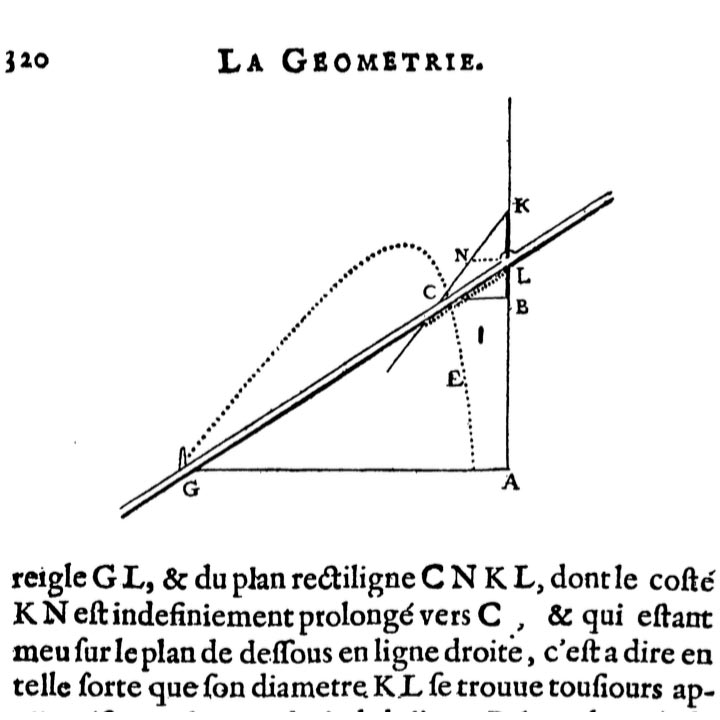
Representation of Nature, for explanation
Bivariate Plot
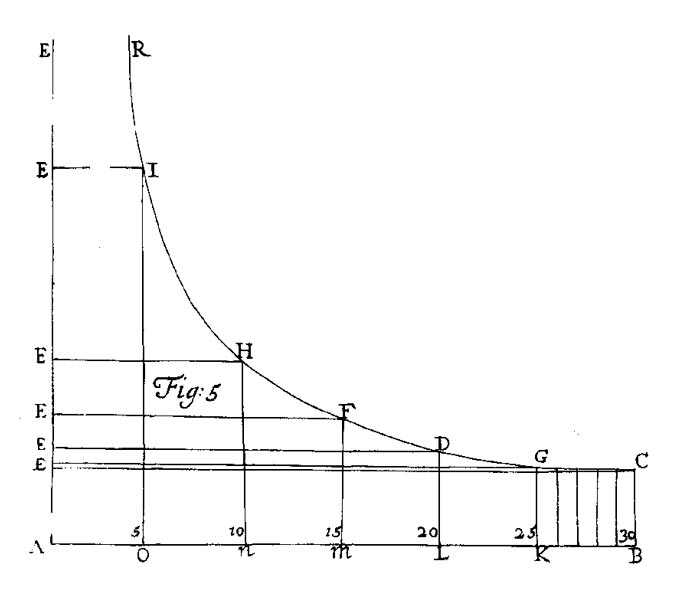
In 1686, E. Halley plotted barometric pressure vs. altitude. A theoretical curve based on observations.
Plots
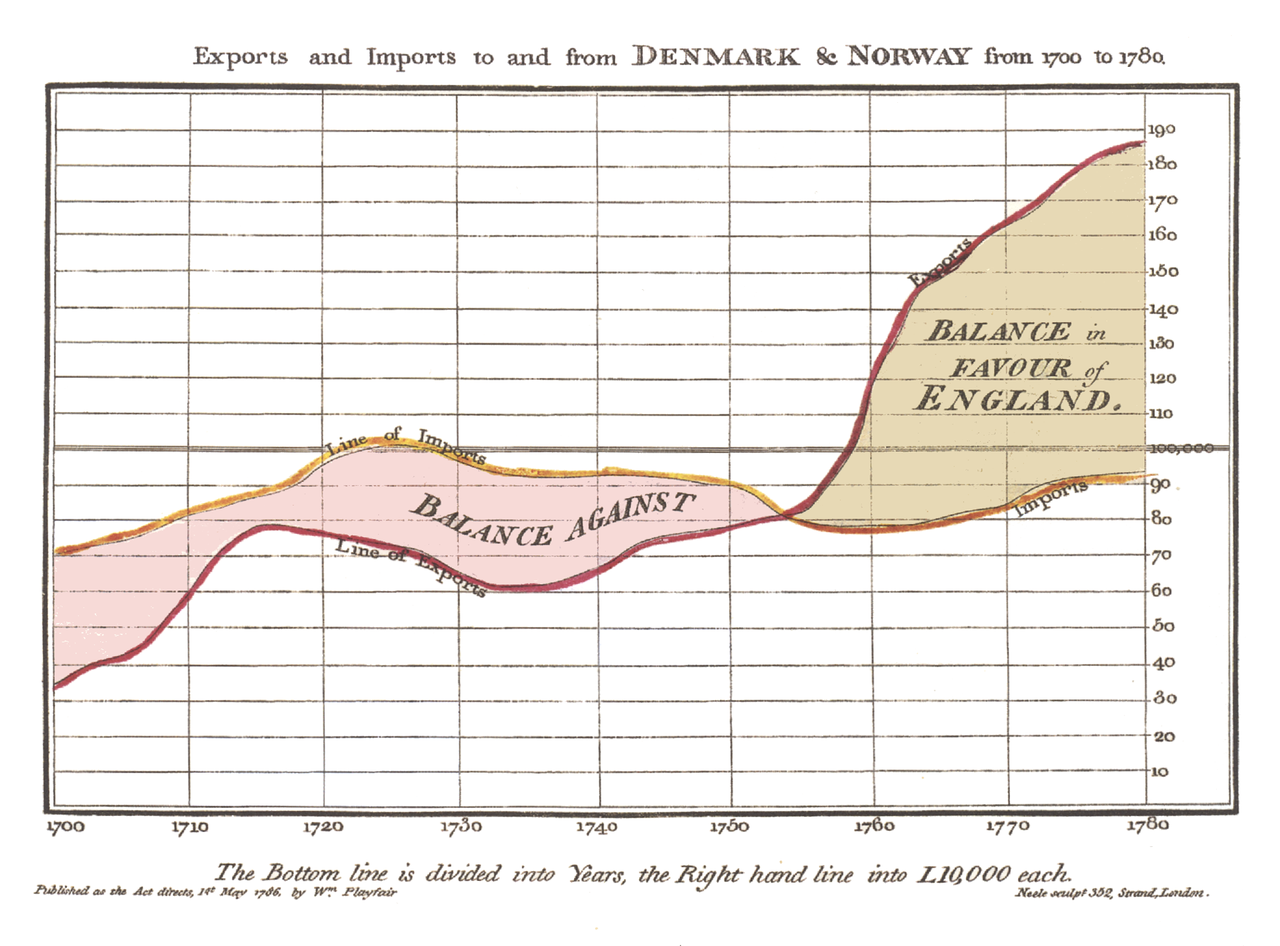
Abstract Graphical Representations
That by means of centripetal forces the planets may be retained in certain orbits, we may easily understand, if we consider the motions of projectiles; for a stone that is projected is by the pressure of its own weight forced out of the rectilinear path, which by the initial projection alone it should have pursued, and made to describe a curved line in the air; and through that crooked way is at last brought down to the ground; and the greater the velocity is with which it is projected, the farther it goes before it falls to the earth. We may therefore suppose the velocity to be so increased, that it would describe an arc of 1, 2, 5, 10, 100, 1000 miles before it arrived at the earth, till at last, exceeding the limits of the earth, it should pass into space without touching it.
-Newton, System of the World
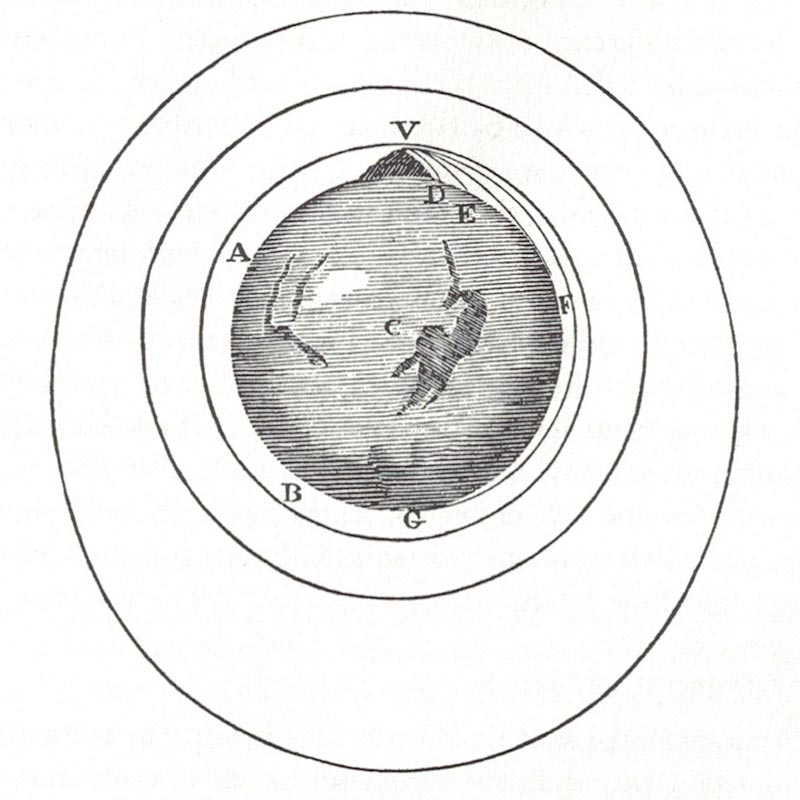
J. C. Maxwell's Thermodynamic Surface, 1874
Visualizations of Experimental Data
Star Map
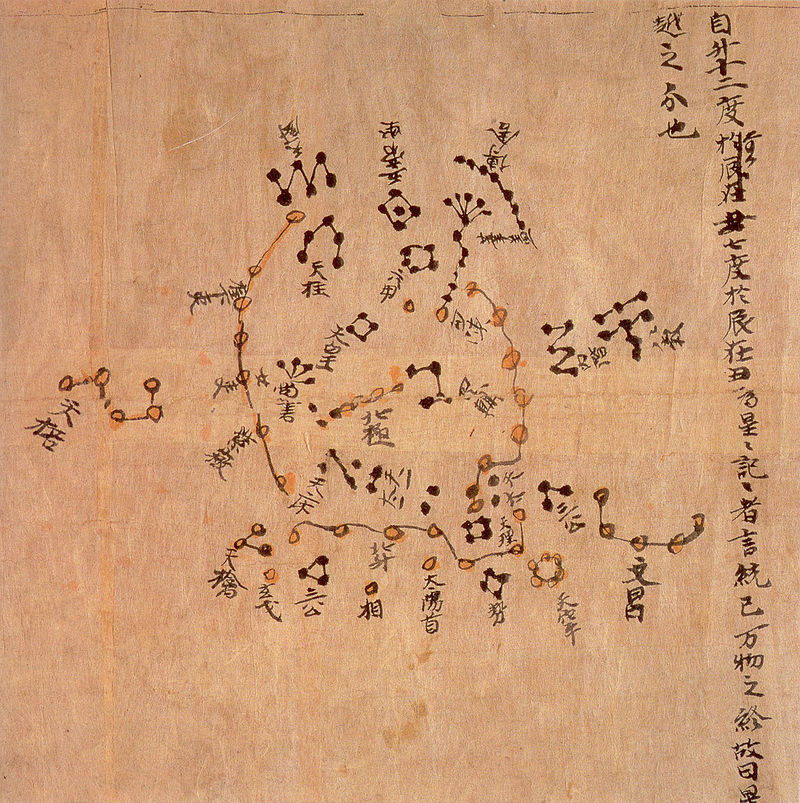
Dunhuang Star Chart, ~ 700 AD
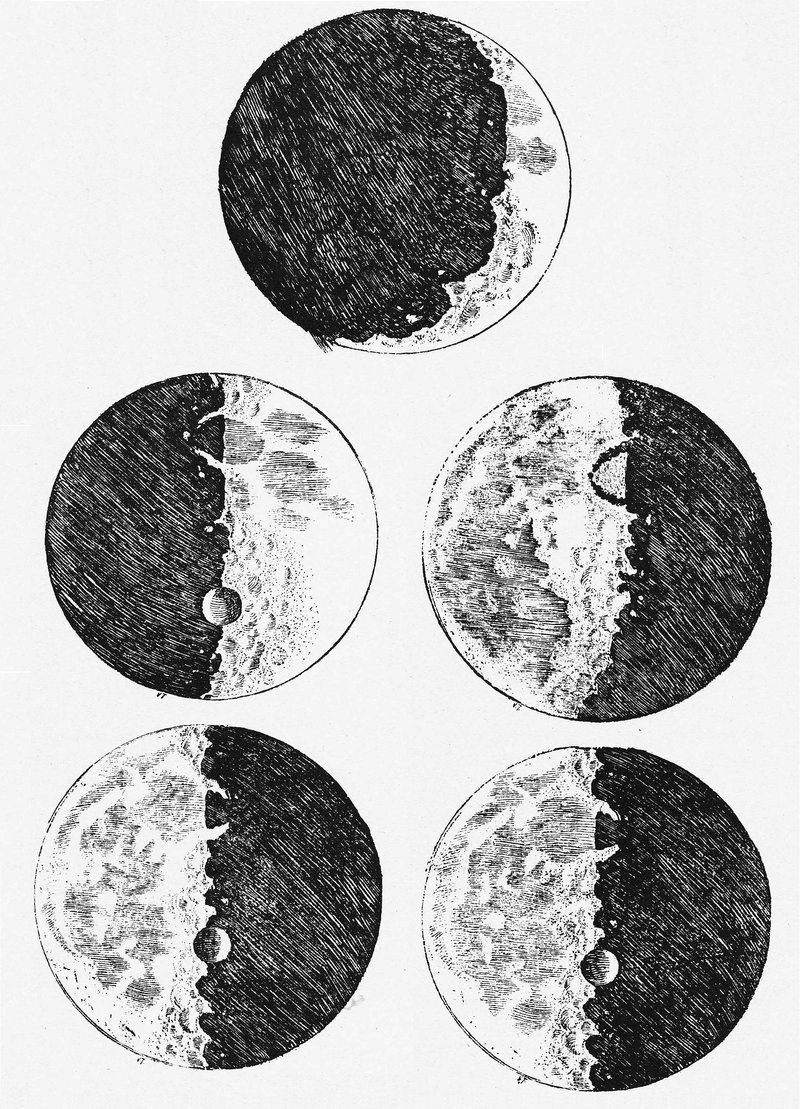
Telescope

Microscope
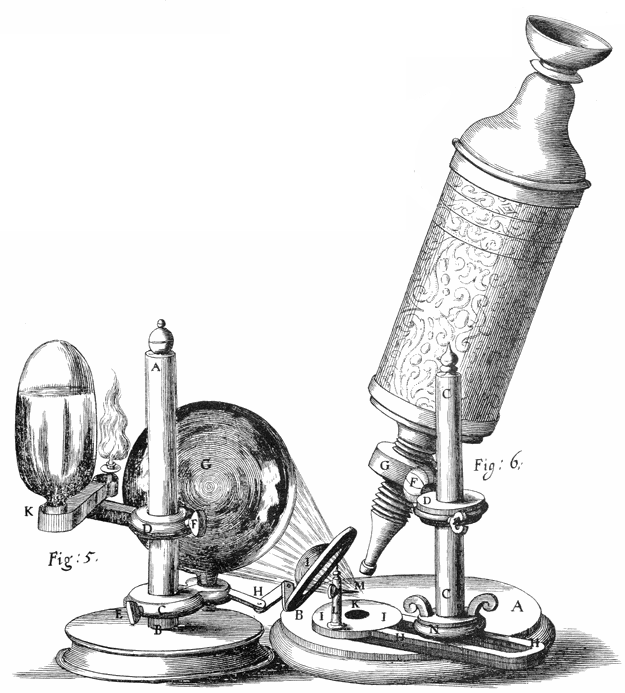
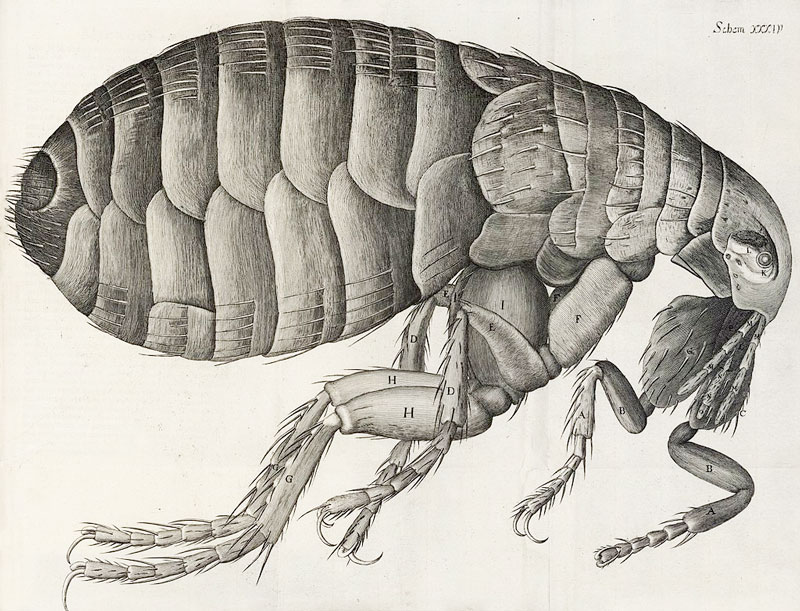
Sometimes we are deceived

Nicolaas Hartsoeker (26 March 1656, Gouda – 10 December 1725, Utrecht) Dutch Mathematician and Physicist.
SPM

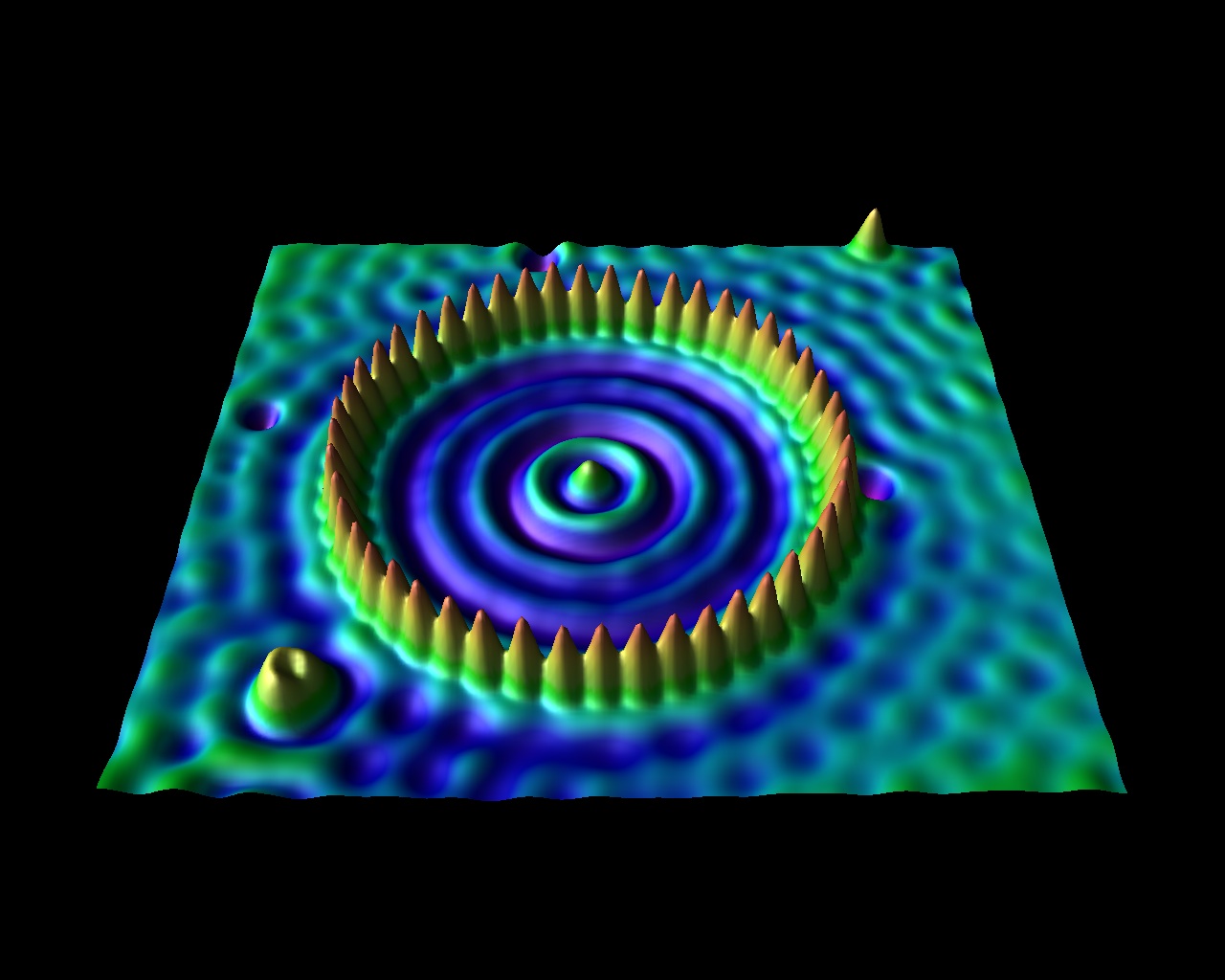
Iron Atoms on Copper surface (1993)
Weather
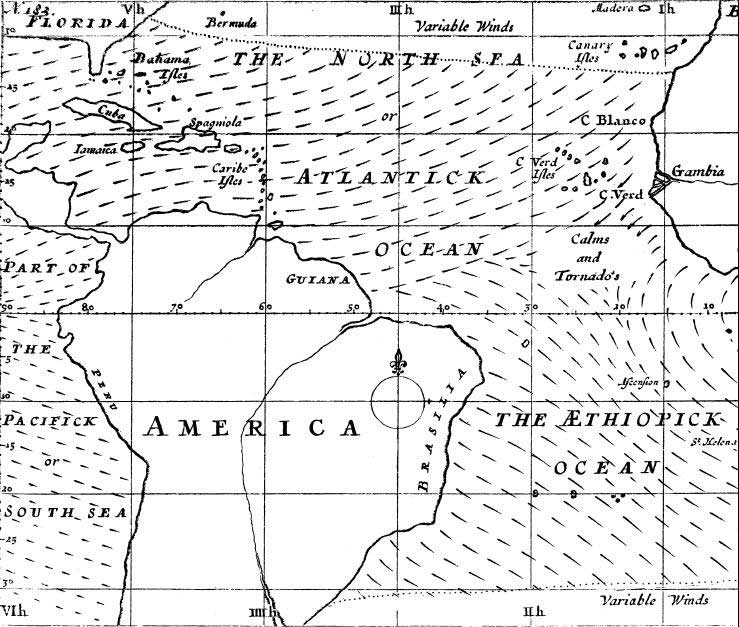
E. Halley (again) First Weather Map. 1686
Wind
Visuals for Learning

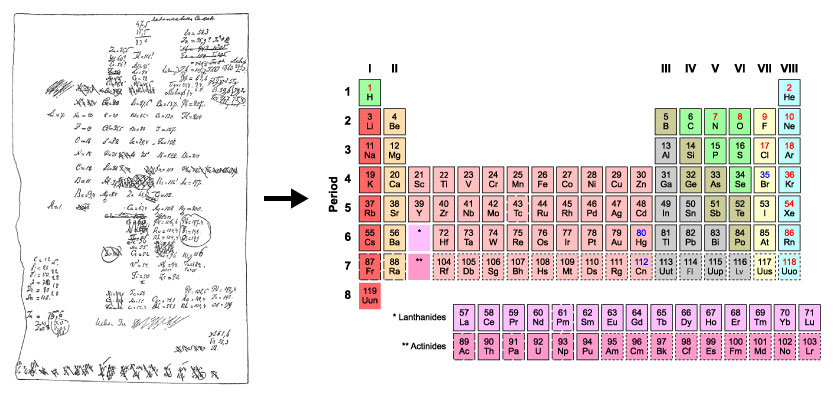
The Periodic Table
Lewis Structures
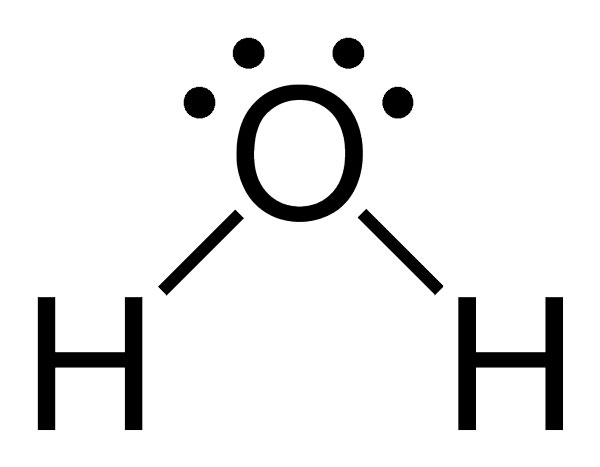
Biology
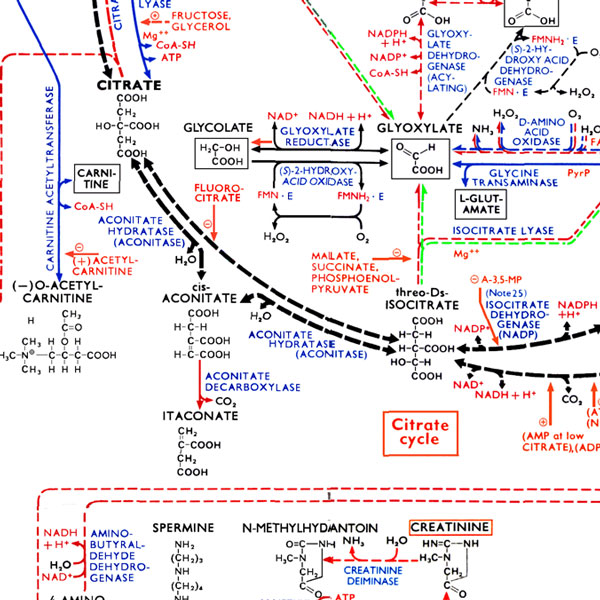
Physics
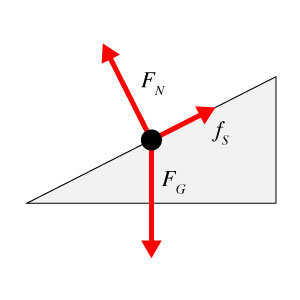
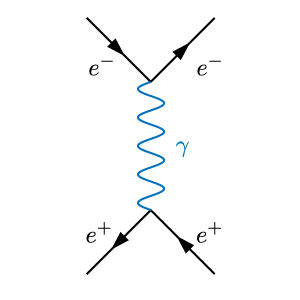
Sims for Basic (and advanced) Physics
What's a sim?
A sim uses animations or other visuals to represent physical phenomenon or concepts.

The Technology
There are many, many sims out there. (Why do we need any more?)
Early Days
P5.js
function setup () {
\\inside this part goes things we need it to do once
}
function draw() {
\\inside this part goes things we need it to do over and over
}
Anyone can make these!
Example: Basic Kinematics
Let's make a bouncy ball
How Motion is Coded
How Acceleration is Coded
Something's not quite right
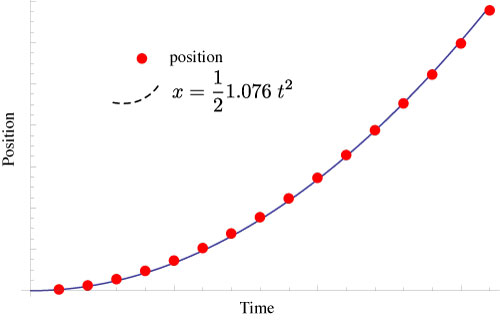
We plot the position of the ball as a function of time.
Compare two versions
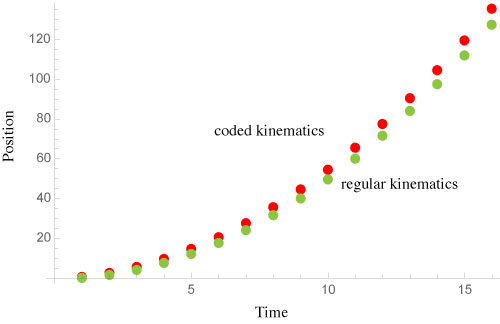
| t | position (good) | position (bad) |
|---|---|---|
| 0 | 0 | 0 |
| 1 | 0.5 | 1 |
| 2 | 2.0 | 3 |
| 3 | 4.5 | 6 |
| 4 | 8.0 | 10 |
| 5 | 12.5 | 15 |
What is acceleration?
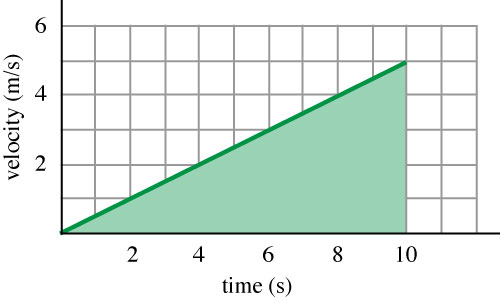
Acceleration implies a change in velocity.
Def. of velocity: $$v = \frac{dx}{dt}$$ or $$x = \int v \;dt = \textrm{area under v(t) curve}$$
Wrong
x += v;
v += a;
ellipse(x,height/2,10,10);
Right
x += averageVelocity;
v += a;
ellipse(x,height/2,10,10);
Acceleration that works!
Happy Bouncer
Science.js
We're building a library of useful science objects.
- Motion objects
- Forces
- Springs
- Graphs
- Optics
- Fields
The goal
1. Build sims for learning
sciencesims.com
2. Learn physics by building sims.
“If you can't explain it to a six year old, you don't understand it yourself.”
- Many people
Virtual Reality



What cool?
3d immersive space.
Phones can run these.
What's not cool?
- Coding is a wee bit harder
- Hardware is still a wee bit expensive.
- Too many wires.
The future??
Refs.
Available upon request.