Imagine a spacecraft on a trip from the earth to the moon. (You can ignore the other bodies in the solar system, i.e. the sun). Exactly halfway between the earth and the moon, the net gravitational force acting on a spacecraft will be:
- Directed towards the Earth
- 0
- Directed towards the Moon
- Directed towards the velocity of the spacecraft.
Which is stronger, the gravitational force the earth exerts on an apple? Or the force the apple exerts on the earth?
- The force that the apple exerts on the earth is stronger
- The force that the earth exerts on the apple is stronger
- The two forces mentioned are equal in magnitude.
- We can't say unless we know the exact masses of each thing.
When two masses are located a distance $d_1$ apart (as measured from their centers), the force of Gravity between them is found to be given by a force $F_1$. If they are brought closer together so that the distance between them is now $d_2 = d_1/2$, i.e. the distance has been decreased by half, what is the new force $F_2$ in terms of the original force, $F_1$?
- $F_2 = F_1$
- $F_2 = 2 \times F_1$
- $F_2 = \frac{1}{2} \times F_1$
- $F_2 = 4 \times F_1$
In the equation for the force of gravity on an person near the surface of the Earth $F = mg$, which of the following does not affect the value of the little $g$.
- The mass of the earth
- The mass of the person
- The radius of the Earth
- The universal gravitational constant, $G$.
Regarding the Earth in its orbit around the sun, which one of the following is true:
- The Earth follows the path of a perfect circle.
- The Earth's speed never changes
- The Earth's distance to the sun changes
- The Sun doesn't experience any gravitational force from the Earth.
If a rock is released from a height 10 meters above the ground and let fall we can obtain a value for the force of gravity acting on the rock and then use Newton's second law to figure out the rock's acceleration, usually called little $g$ which has an approximate value of 9.8 m/s2. How would that acceleration change if we dropped the rock from a height of 10 kilometers.
- The rock's acceleration would be exactly the same
- The rock's acceleration would be slightly less than $g$.
- The rock's acceleration would be slightly greater than $g$.
- The rock's acceleration would be about 1,000 times less than $g$.
Three masses are in deep space. The two large masses, each of mass $m$, are located equal distances away from the x axis both at x = 0. A third mass, $m_0$ is located on the x axis as shown. In which direction is the net gravitational force acting on $m_0$?
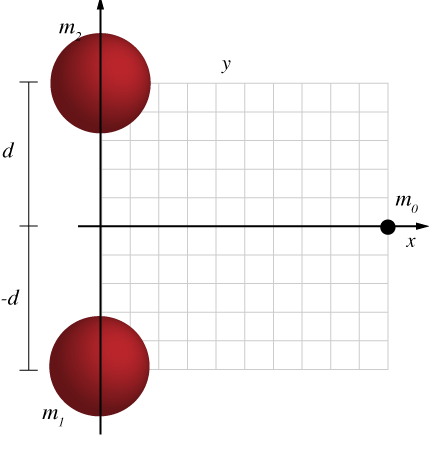
- +x
- -x
- A mix of x and y
- No direction since the net force is zero.
How does the gravitational force between the Earth and the Sun change over a year?
- It doesn't since the masses of the two objects are constant.
- It's greater during the times of year when the Earth is closer to the sun.
- It's greater during the times of year when the Earth is farther from the sun.
- It doesn't because the distance to the sun is always the same.
The picture below shows a simplified model of the Earth orbiting the Sun. A coordinate system is shown as well in blue. At the point in time shown, what vector direction would best describe the direction of the acceleration of the Earth.
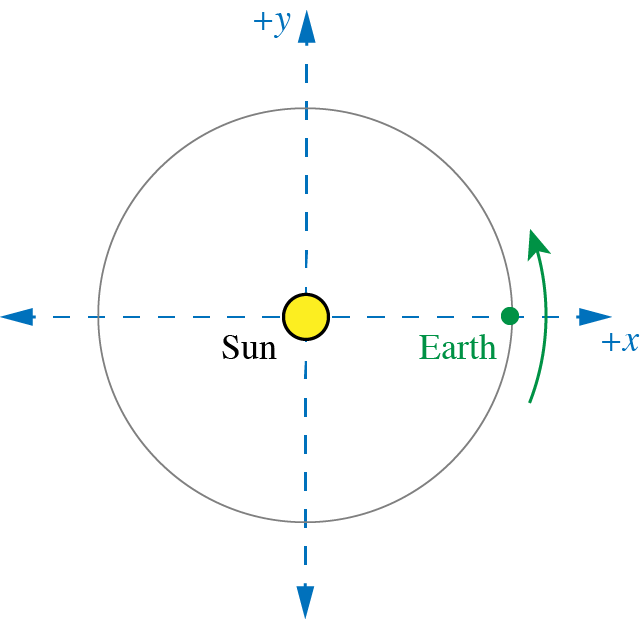
- No direction since the Earth is not accelerating.
- In a direction that has both -x and +y components.
- In the -x direction.
- In the +y direction.
If you are standing in an elevator and the normal force between you and floor is greater than the force of gravity acting on you from the Earth, what can you assume to be happening? (Let +y be pointed away in the traditional up direction.)
- The elevator is moving in -y at constant speed.
- The elevator is moving up +y constant speed.
- The elevator is accelerating in the -y direction.
- The elevator is accelerating in the +y direction.
A communications satellite is in low earth orbit, which means it is orbiting at a height of a few hundred miles or so above the surface of the Earth. The time it takes for the satellite to orbit the Earth once (called the orbital period) is about 90 minutes. If the satellite used its thrusters to move into a higher orbit, further away from the earth, what can say about its orbital period?
- The period would remain constant since the mass of the satellite isn't changing.
- The period would increase since the force acting on the satellite has decreased.
- The period would decrease since the force acting on the satellite has decreased.
- The period would remain constant since the force is also constant.
If a 10 year old asked you "Why do bowling balls fall faster than feathers when I drop them?" which would be the most physically correct explanation.
- Bowling balls have more mass and thus experience more acceleration due to gravity.
- Feathers are lighter and thus experience less acceleration due to gravity.
- Bowling balls are made of metal and metal is attracted to the ground more than feather materials
- Feathers get blocked by air molecules more than bowling balls do and that's what slows them down.

