Stellar Interiors
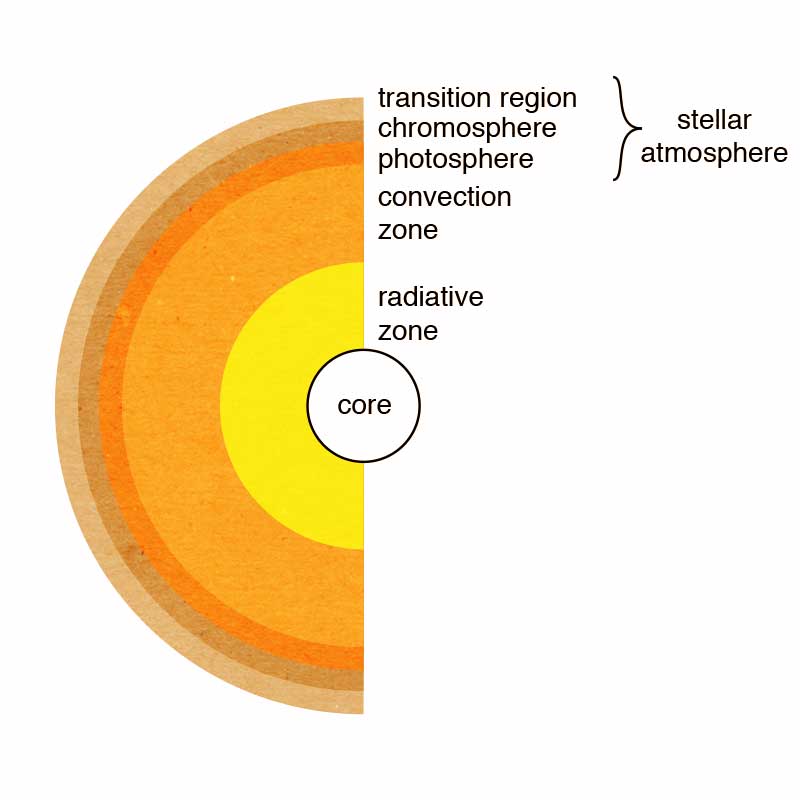
The basic structure of a star.
Hydrostatic Equilibrium
A small volume of gas has three force vectors acting in the vertical directions: gravity, pressure from below and pressure from above.
Let's imagine a small cylindrical volume of gas that is located in a larger region. There will be three forces acting on it: $F_\textrm{grav}$ is the force of gravity, and two forces from the pressure, one from the pressure above: $P + \Delta P$ and one from pressure below: $P$. The net force from the pressure will be : $$\begin{equation} F_\textrm{pres} = A[ P - (P + \Delta P)] \end{equation}$$ where $A$ is the area (whose surface normal points in the y direction) of the gas volume. The gravitation force will be given by: $$\begin{equation} F_\textrm{grav} = -\frac{G M_r \rho A \Delta r}{r^2} \end{equation}$$ where $M_r$ is the mass enclosed by a sphere of radius $r$ centered about the earth's center.
If this volume of gas is in equilibrium, then the pressure forces and the gravitational forces will be equal: $$\begin{equation} A[ P - (P + \Delta P)] - \frac{G M_r \rho A \Delta r}{r^2} = 0 \end{equation}$$ Solving for $\Delta P$: $$\begin{equation} \Delta P = -\frac{G M_r \rho }{r^2} \Delta r \end{equation}$$ If we consider this cylinder to be infinitely thin: $\Delta r \rightarrow =0$, then we have a differential form: $$\begin{equation} \frac{dP}{dr} = -\frac{G M_r \rho }{r^2} \label{eq:hydrostaticequilibrium} \end{equation}$$ Eq. \eqref{eq:hydrostaticequilibrium} is called the equation of hydrostatic equilibrium (for a spherical symmetric body).
To apply this to a star, we should acknowledge the limiting assumptions we made:
- The star is spherical
- The star is not rotating
- The star is not expanding or contracting
- Gravity and Pressure gradients are the only forces acting.
\begin{equation} \frac{dP}{dr} = -\frac{G M_r \rho }{r^2} \end{equation}
Pressure in the sun
Find a rough estimate for the pressure at the center of the sun.
Pressure-radius
A better way to write this would be to include the dependencies: $$\begin{equation} \bbox[10px,border:2px solid red]{\frac{dP}{dr} = -\frac{G M(r) \rho(r) }{r^2}} \label{eq:hydrostaticequilibriumdep} \end{equation}$$Mass continuity
$$\begin{equation} \bbox[10px,border:2px solid red]{\frac{dM}{dr} = 4 \pi r^2 \rho(r)} \end{equation}$$Stellar Energy Sources
Where does it come from?
The first suggestion to explain where stars got the energy was to look at the gravitational potential. Let's say we have two particles, then the gravitational potential energy between them is: $$\begin{equation} U = -G\frac{M m}{r} \end{equation} $$
How much energy is there in gravity?
Of course there are more than two particles in a star, so we'll have to expand that equation a bit. If a point mass $dm$ is located outside a spherically symmetric mass $M_r$, then the force on that point mass will be directed to the center and will have a magnitude: $$\begin{equation*} dF_{g,i} = G \frac{M_r dm_i}{r^2} \end{equation*}$$ The potential energy of the point mass is thus: $$\begin{equation} dU_{g,i} = - G \frac{M_r dm_i}{r} \label{eq:pointGravPot} \end{equation}$$ Now we'll consider a shell of thickness $dr$ and mass $dm$: $$\begin{equation*} dm = 4 \pi r^2 \rho dr \end{equation*}$$ where $\rho$ is the density and $4 \pi r^2 dr$ is the volume of the shell. Thus, eq \eqref{eq:pointGravPot} becomes $$\begin{equation*} dU_g = - G \frac{M_r 4 \pi r^2 \rho}{r}dr \end{equation*}$$
We can integrate over the radius of the star $R$ like this: $$\begin{equation} U_g = -4 \pi G \int_0^R M_r \rho r \;dr \label{eq:integrateGravPot} \end{equation}$$ Of course we probably don't know $\rho$ very well at this point, but we can guess based on it's average value: $$\begin{equation*} \rho \sim \bar{\rho} = \frac{M}{\frac{4}{3}\pi R^3} \end{equation*}$$ with $M$ being the total mass of the star. Also: $$\begin{equation*} M_r \sim \frac{4}{3}\pi r^3 \bar{\rho} \end{equation*}$$ Putting this into eq. \eqref{eq:integrateGravPot}, we get: $$\begin{equation} U_g \sim \frac{16 \pi^2}{15}G \bar{\rho}^2 R^5 \sim -\frac{3}{5}\frac{GM^2}{R} \end{equation}$$
Applying the virial theorum, we have: $$\begin{equation} E \sim - \frac{3}{10}\frac{GM^2}{R} \end{equation}$$
If we plug some sun values into this: $$\begin{equation*} \frac{3}{10}\frac{G M_\unicode{x2609}^2}{R_\unicode{x2609}} \approx 1.1 \times 10^{41} \; \textrm{J} \end{equation*}$$ Now if the sun luminosity was constant at today's value: $3.84 \times 10^{26} \; \textrm{W}$, then this would mean there is enough energy to last for about $1 \times 10^{7}$ years (about 10 million years). This is notably too short given other observations from geology that suggest the earth and moon and things have been around for billions of years. There must be another source of energy contributing to the star's luminosity.
Intro to Nuclear Reactions
Fission
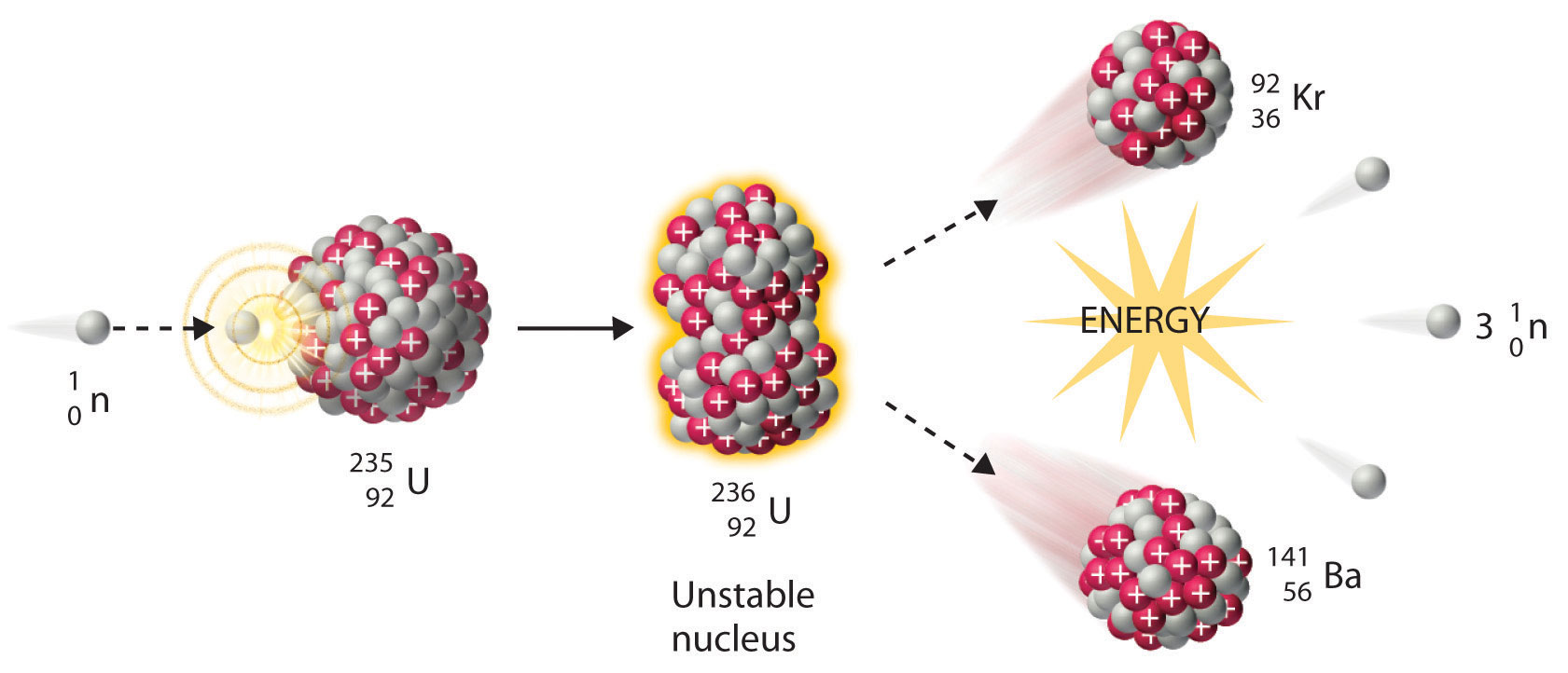
http://www.nuclear-power.net/nuclear-power/fission/
Fusion

http://www.nuclear-power.net/nuclear-power/nuclear-fusion/
Take four Hydrogen atoms (1 proton & 1 electron), each have a mass of 1.00782503214 u. Together, they therefore have a combined mass of 4.03130013 u. One Helium-4 atom has a mass of 4.002603 u. This is obtained by adding the mass of the neutrons and the protons together. Thus, let's say we were able to mash 4 Hydrogen atoms together and make a Helium. Now there would be a change in mass between the initial and final constitutions: $\Delta m = 4.03130013 - 4.002603 = 0.028697 \; \textrm{u}$.
Since $E = mc^2$, we can see that this amount of mass is associated with an energy of 26.731 MeV. This is essentially the amount of energy released in the formation of a Helium nucleus, aka the binding energy. (This is also the amount of energy that would be required to take apart a Helium nucleus.) The trick is to figure out exactly how we can combine 4 Hydrogen atoms to make a Helium. (that's the study of High energy physics earlier last century)
Fundamental Forces
| Force | Relative Strength | Distance | What does? |
|---|---|---|---|
| Weak | 1033 | 10-18 | Radioactive Decay |
| Strong | 1038 | 10-15 | Keeps atomic nuclei together |
| Gravity | 1 | ∞ | Brings everything together |
| Electromagnetic | 1036 | ∞ | Chemistry, charges, etc |
The Isotopes of Hydrogen
Binding Energies

Bringing them together
The plots of the Coulomb force (top) and the Coulomb potential (bottom).
One impediment is the Coulomb repulsion between two protons, both of which are positively charged.
Tunneling
A 1-d simulation of a wave packet incident on a potential barrier. Some of the wave tunnels through the barrier.
Criteria for tunneling: a) the distance between protons should be comparable to the de Broglie wavelength: $$\begin{equation} \lambda_{DB} = \frac{h}{p} = 7 \times 10^{-13} \; \textrm{m} \end{equation}$$
and b) the kinetic energy ($E$) of the proton needs to be comparable to the electrostatic potential energy at that separation. $$\begin{equation} U = \frac{e^2}{4 \pi \epsilon_0} \frac{1}{\lambda_{DB}} = \frac{e^2}{4 \pi \epsilon_0} \frac{(2 m_p E)^{1/2}}{h} \approx E \end{equation}$$
Energy / Tunneling
A qualitative graph showing the what happens when two protons get close enough for the strong force to dominate.
Cross Section, basics
Apples in a tree
We can say each apple has a cross-section of: $$ \sigma = \pi r^2 $$ If we shoot 200 arrows into the tree, how many apples will we hit? $$ N_\textrm{hit} = N_\textrm{inc} * n_\textrm{tar} * \sigma $$ where $n_\textrm{tar} = \frac{\textrm{number of apples}}{\textrm{area of tree}}$ and $n_\textrm{inc} = \textrm{# incident arrows = 200}$ If $r = 0.1$ and $R = 5.0$ then, $$ N_\textrm{hit} = 200 \times \frac{13}{\pi \; 5.0^2} \times \pi \; 0.1^2 $$
Or, we can divide the number of apples by a $\Delta t$ to get a rate, then we would have a rate of apple hits: $$\frac{N_\textrm{hit}}{\Delta t} = \frac{N_\textrm{inc}}{\Delta t} * n_\textrm{tar} * \sigma$$
Cross Section
The cross section gives a probability of interaction. It is the number of reactions per target nucleus per time divided by the flux of incident particles.
$$\begin{equation*} \sigma(E) \equiv \frac{\textrm{number of reactions/nucleus/time}}{\textrm{number of incident particles/area/time}} \end{equation*}$$Cross Section
Imagine a cylinder of length $ds = v(E) dt$ and area $\sigma(E)$.
$n$ : just a particle
$n_i$ : an incident particle
$n_{iE}dE$ : # of incident particles having energies between $E$ and $E+dE$ per unit volume
$dN_E$ : # of particles that "hit the wall" / time or # of reactions / time
$n_E dE$ : # of particles with an energy between E and $E+dE$, (might not be incident)
If a particle hits the wall, then there is a reaction. This is an abstraction of the nuclear collision process. (there is no cylinder, no wall...)
We have a target particle ($x$) and an incident particle ($i$). If the incident particle strikes the area $\sigma(E)$, then there will be a nuclear reaction.
Take the number of incident particles per unit volume having energy between $E$ and $E+ dE$ to be: $n_{iE} dE$. (This is like a density) To find the number of such particles inside the cylinder: $$\begin{equation*} dN_E = \underbrace{n_{iE} dE}_{\textrm{density}} \;\; \underbrace{\sigma(E) v(E) dt}_{\textrm{volume}} \end{equation*}$$ The number of particles with the appropriate kinetic energy is some fraction of the whole: $$\begin{equation*} n_{iE} dE = \frac{\int_0^\infty n_{iE} dE}{\int_0^\infty n_E dE} n_E dE = \frac{n_i}{n}n_E dE \end{equation*}$$
where $n_E dE$ is given by the Maxwell-Boltzmann distribution $$\begin{equation} n_E dE = \frac{2n}{\sqrt{\pi}} \left(\frac{1}{kT}\right)^{3/2} \, E^{1/2}e^{- \frac{E}{kT}} dE \label{eq:maxwell-boltzmann-distribution} \end{equation}$$
The number of reactions per target nucleus per time $dt$ having energies between $E$ and $E+dE$ is $$\begin{equation*} \frac{ \textrm{reactions per nucleus}}{\textrm{time interval}} = \frac{dN_E}{dt} = \sigma(E)v(E)\frac{n_i}{n}n_E dE \end{equation*}$$ Lastly, if there are $n_x$ targets per unit volume, then the total number of reactions per unit volume per unit time, given all possible energies is: $$\begin{equation} r_{ix} = \int_0^\infty n_x n_i \sigma(E) v(E) \frac{n_E}{n}dE \end{equation}$$
$\sigma(E)$
But, what exactly is $\sigma(E)$?
Should be in the order of the de Broglie $\lambda$ $$\begin{equation} \sigma(E) \propto \pi \lambda_{DB}^2 \propto \pi \left( \frac{h}{p}\right)^2 \propto \frac{1}{E} \label{eq:sigmaE1} \end{equation}$$ (Since $K = E = \mu_m v^2 / 2 = p^2 / 2\mu_m$)
Also, for a barrier $U$ and particle with energy $E$, the probability for tunneling through will go as: $$\begin{equation} \sigma(E) \propto e^{-2 \pi^2 U/E} \end{equation}$$ In this case the $U$ is the Coulomb potential: $U_c = \frac{Z_1 Z_2 e^2}{4 \pi \epsilon_0 r}$ and $E$ is just the kinetic energy: $E = \mu_m v^2 / 2$. We can assume the distance $r$ is basically the de Broglie wavelength: $r \sim \lambda = h/p$.
In which case we obtain: $$\begin{equation} \sigma(E) \propto e^{-bE^{-1/2}} \label{eq:sigmaE2} \end{equation}$$ where $b$ is given by $$\begin{equation*} b \equiv \frac{\pi \mu_m^{1/2} Z_1 Z_2 e^2}{2^{1/2} \epsilon_0 h} \end{equation*}$$
We can combine eq \eqref{eq:sigmaE1} and \eqref{eq:sigmaE2} and add another function $S(E)$ (that doesn't change much) to get a functional form for $\sigma(E)$: $$\begin{equation} \sigma(E) = \frac{S(E)}{E}e^{-b E^{-1/2}} \end{equation}$$
Finally, we can write a reaction rate as: $$\begin{equation} r_{ix} = \left( \frac{2}{kT}\right)^{3/2} \frac{n_i n_x}{(\mu_m \pi)^{1/2}} \int_0^\infty S(E) e^{-b E^{-1/2}} e^{-E/kT} dE \end{equation}$$
The likelihood that a nuclear reaction will occur.
The peak will be at $$\begin{equation} E_0 = \left( \frac{bkT}{2}\right)^{2/3} \end{equation}$$

The 7th Solvay Conference
https://catalog.archives.gov/id/7665680

p-p chain
The full p-p chain
$4 \; {}^1_1 \textrm{H} \rightarrow {}^4_2 \textrm{He} + 2e^+ + 2\nu_e + 2\gamma$
| $e^+$ | positron |
| $\nu_e$ | electron nutrino |
| $\gamma$ | gamma ray |
CNO Cycle
The CNO cycle
Luminosity Gradient
$$\begin{equation} dL = \epsilon \; dm \end{equation}$$Here, $\epsilon$ is the total energy released per kilogram per second by all the star stuff: gravity and nuclear reactions together.
For spherically symmetric star, the mass of a thin shell of thickness $dr$ will be: $$\begin{equation} dm = dM_r = \rho dV = 4\pi r^2 \rho dr \end{equation}$$
which leads to: $$\begin{equation} \frac{dL_r}{dr} = 4 \pi r^2 \rho \epsilon \label{eq:luminosity-gradient} \end{equation}$$Energy Transport
Radiative
Radiation Pressure
A thin spherical shell centered on the star center. Let $dr \ll r$
The radiation pressure on the inner surface: $$\begin{equation} P_\textrm{rad}(r) = \frac{a T^4}{3} \label{eq:pradinner} \end{equation}$$ The radiation pressure on the outer surface: $$\begin{equation} P_\textrm{rad}(r+dr) = \frac{a (T+dT)^4}{3} = \frac{a}{3}T^4 \left( 1 + \frac{dT}{T}\right)^4 \approx \frac{a}{3}T^4 \left( 1 + 4 \frac{dT}{T}\right) \label{eq:pradouter} \end{equation}$$ (assuming $dt/T \ll 1$)
Thus, the net radiation force will be given by: $$\begin{equation} F_\textrm{rad} = [ P_\textrm{rad}(r)-P_\textrm{rad}(r+dr) ] 4 \pi r^2 \end{equation}$$ which using eqs. \eqref{eq:pradinner} and \eqref{eq:pradouter}, we can get: $$\begin{equation} F_\textrm{rad} \approx - \frac{a}{3}4 T^4 \frac{dT}{T}4 \pi r^2 = - \frac{16 \pi}{3}a r^2 T^3 dT \label{eq:radiationforceonshell} \end{equation}$$
The optical depth is given by: $$\begin{equation} d \tau = - \rho(r) \kappa(r) dr \end{equation}$$ where $\kappa$ is the opacity. The probability that a photon will be absorbed while passing through the shell is $dP \approx d\tau$.
The rate at which photons carry energy through the shell is the luminosity, $L(r)$. Momentum is carried through the shell is just $L(r)/c$, since $p = E/c$.
The force on the shell, i.e. the rate at which photon momentum is transferred to the shell will be $$\begin{equation} F_\textrm{rad} = \frac{L(r)}{c}d\tau = - \frac{L(r)}{c}\rho(r)\kappa(r)dr \label{eq:fradandLum} \end{equation}$$ Combing eq. \eqref{eq:fradandLum} equation with eq. \eqref{eq:radiationforceonshell}, we get: $$\begin{equation} - \frac{16 \pi}{3}a r^2 T(r)^3 dT = - \frac{L(r)}{c}\rho(r)\kappa(r)dr \end{equation}$$
This can be rearranged to yield the equation of radiative energy transport: $$\begin{equation} \frac{dT}{dr} = - \frac{3 \rho(r) \kappa(r) L(r)}{16 \pi a c \; T(r)^3 r^2} \end{equation}$$
This equation related the luminosity to the temperature gradiant of a star.
Convective Transport
This is the equation of convective energy transport. $$\begin{equation} \frac{dT}{dr} = \left( 1-\frac{1}{\gamma}\right)\frac{T(r)}{P(r)}\frac{dP}{dr} \end{equation}$$ It shows that the temperature gradient is proportional to the pressure gradient. ($\gamma$ is the adiabatic index and depends on the gas in question. )
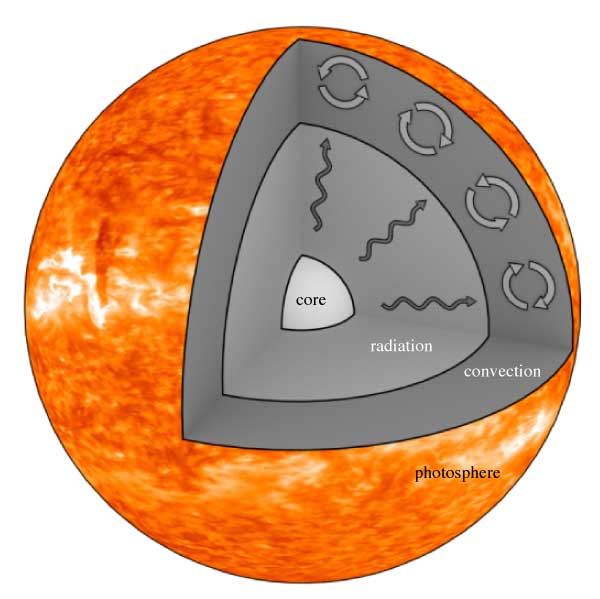
The different transport modes are separated into regions.
Stellar Model Building
$$\begin{align*} \frac{dP}{dr} & = -\frac{G M_r \rho }{r^2} \\ \\ \frac{dM}{dr} & = 4 \pi r^2 \rho(r) \\ \\ \frac{dL}{dr} & = 4 \pi r^2 \rho(r) \epsilon(r) \\ \\ \frac{dT}{dr} & = - \frac{3 \rho(r) \kappa(r) L(r)}{16 \pi a c \; T(r)^3 r^2} \;\; \textrm{[for radiative]}\\ \\ & = \left( 1-\frac{1}{\gamma}\right)\frac{T(r)}{P(r)}\frac{dP}{dr} \;\; \textrm{[for convective]} \end{align*}$$Boundary Conditions
In order to solve these equations, we need boundary conditions: At the center we should expect: $$ \left. \begin{array}{l} M_r & \rightarrow 0 \\ L_r & \rightarrow 0 \end{array} \right\} \textrm{as}\;r \rightarrow 0 $$ and at the surface of the star: $$ \left. \begin{array}{l} T & \rightarrow 0 \\ P & \rightarrow 0 \\ \rho & \rightarrow 0 \end{array} \right\} \textrm{as}\;r \rightarrow R_* $$