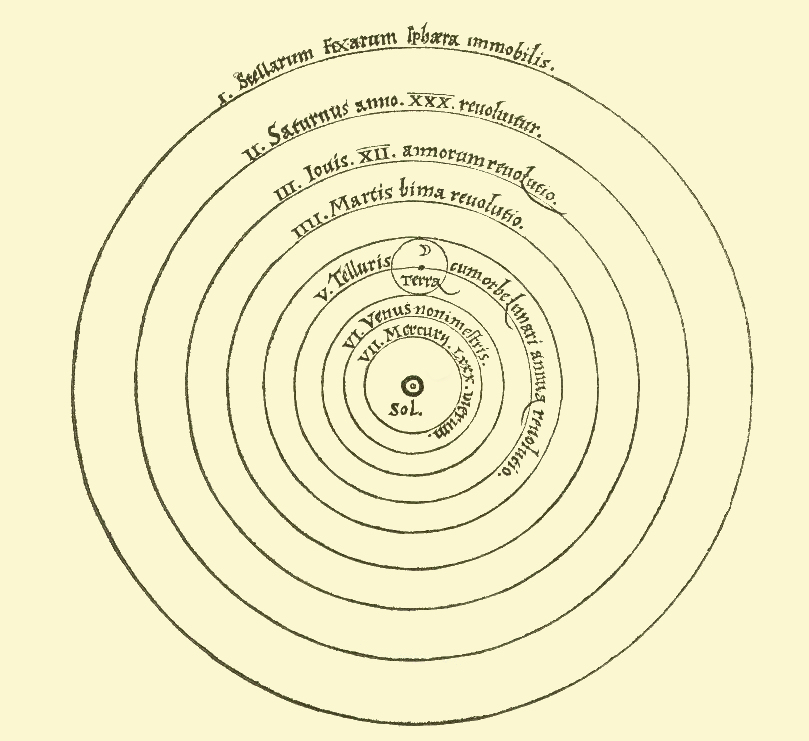
Why circles?
The Copernican System consisted of circular orbits centered around the sun.
Copernicus was right: the earth and the other planets do orbit around the sun. However, he was still operating under the assumption that all the celestial bodies had to move in perfect circles. This turned out to be a rather major flaw in the framework.
Other astronomers of the era were unable to match the predictions of the Copernican system with observations. More 'tweaks' were added to the Copernican systems of circular heliocentric orbits in order to 'save the appearances'. In order to make the model match with observations, they still had to employ epicycles and so forth. However, the seed was planted. The sun should be at the center!
Tycho Brahe
Danish astronomer Tycho Brahe [1546-1601]. Made many very good measurements of the stars and planets.
Late 16th century. Hybrid system: geoheliocentric model had the planets going around the sun, but the sun still went around the Earth. Close...
Johannus Kepler
German mathematician, astronomer, and astrologer. [1571-1630] Kepler was Tycho's assistant and was believed in the Copernican system.
Kepler played a major role in the 17th-century scientific revolution. He is best known for his laws of planetary motion, based on his works Astronomia nova, Harmonices Mundi, and Epitome of Copernican Astronomy. These works also provided one of the foundations for Newton's theory of universal gravitation.
Kepler's 3 laws of orbiting bodies
A planet orbits the sun in an ellipse. The Sun is at one focus of that ellipse.
A line connecting a planet to the Sun sweeps out equal areas in equal times
The square of a planet's orbital period is proportional to the cube of the average distance between the planet and the sun: $P^2 \propto a^3$.
Ellipses
An ellipse satisfies this equation:
$$
\begin{equation}
r + r' = 2a
\label{eq:basic-ellipse}
\end{equation}
$$
$a$ is the semi-major axis
$r$ and $r'$ are the distances to the ellipse from the two focal points , $F$ and $F'$.
$e$ represents the eccentricity of the ellipse ($0 \leq e \leq 1$)
Conic Sections
The circle is one of several conic sections. (There's really nothing all that special about circles.)
Elliptical Orbits
The first law for Kepler holds that the orbiting body (i.e. planet) will trace out an elliptical path as it orbits the central body (i.e. the sun). The central body is located at the principle focus . When the distance between the planet and the sun is the shortest, the planet is said to be at perihelion , or the point of closes approach. When that distance is greatest, the planet is located the aphelion .
Polar Coordinates
$$
\begin{equation}
r = \frac{a\left( 1-e^2\right)}{1+e \cos \theta}
\label{eq:polar-equation-ellipse}
\end{equation}
$$
Ellipse - the point where $r = r'$
The polar coordinate equation can be obtained by starting with the basic ellipse equation Eq. $\eqref{eq:basic-ellipse}$ Take the point at the top of the semi-minor axis, where $r=r'$. Since $r + r' = 2a$ we know that $r = a$.
Using the Pythagorean theorem, we can say that:
$$r^2 = b^2 + a^2e^2$$
Putting $a$ in for $r$ yields:
$$\begin{equation}
b^2 = a^2(1-e^2)
\end{equation}$$
Or, to have it more explicitely as the ratio of the two axes:
$$
\begin{equation}
e = \sqrt{1-\frac{b^2}{a^2}}
\end{equation}
$$
Ellipse - and polar coordinates $r$ and $\theta$.
For polar coordinates, we'll use $r$ and $\theta$, $r$ being the distance from the principle focus and $\theta$ the angle measured counterclockwise from major axis of the ellipse.
Again, from Pythagorus:
$$r'^2 = r^2 \sin^2 \theta + (2ae + r \cos \theta)^2$$
Expanding the 2nd RHS term:
\begin{align}
\begin{split}
r'^2 & = r^2 \sin^2 \theta + 4a^2e^2 + 4 a e r \cos \theta + r^2 \cos^2 \theta \\
& = r^2+4 a e \left( ae+r\cos \theta\right)
\end{split}
\end{align}
and using the fact that $r'^2 = \left(2a - r\right)^2$, we can obtain the polar equation for the ellipse shown above in eq \eqref{eq:polar-equation-ellipse}.
Deviation from a Circles
Mars' orbit [$e = 0.0934$] looks a lot like a circle.
Equal Areas in Equal Times
The blue areas in these figures will be the same if $t_2 - t_1$ is the same.
Kepler's second law describes the areas swept out by an orbiting planet in a given time and says that for any given interval of time, the areas swept out will always be equal.
The other conics
Parabolas: $e = 1$
$$
\begin{equation}
r = \frac{2 p}{1+\cos \theta}
\end{equation}
$$
Hyperbolas: $e \gt 1$
$$
\begin{equation}
r = \frac{a(e^2-1)}{1+e\cos \theta}
\end{equation}
$$
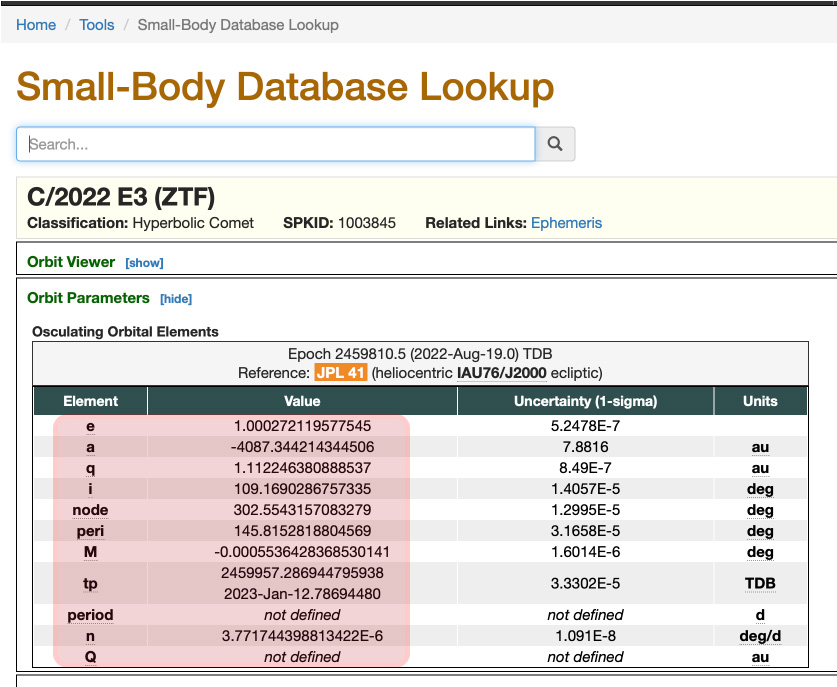
C/2023 E3 ZTF
APOD of the comet
Astronomy Picture of the Day
C/2023 E3 ZTF
Lookup the comet in the small body database
Newton's Laws
In words:
No change in velocity if there is no net force acting.
The net force acting on a body will cause a proportional acceleration inversely proportional to the mass of that body.
Forces come in equal and opposite pairs
In symbols:
$\Delta v = 0 $ if $F_\textrm{net} = 0$
$\mathbf{F}_\textrm{net} = \sum_{i=1}^n \mathbf{F}_i = m\mathbf{a}$
$F_{AB} = -F_{BA}$
Law of Gravitation
Two masses and a gravitational interaction
The scalar form:
$$\begin{equation}
F = G \frac{M m}{r^2}
\end{equation}$$
And in vector form:
$$\begin{equation}
\mathbf{F}_{21} = - G \frac{M m}{r^2}\hat{\bf{r}}
\end{equation}$$
This is Newton's Law of Universal Gravitation . It considers two masses: $M$ and $m$ and the distance between them $r$. Also included is $G$, the Universal Gravitational Constant . ($G = 6.674 \; 08 \times 10^{-11} $ m3 kg-1 s-2 From nist http://physics.nist.gov/cgi-bin/cuu/Value?bg ). The direction of the force is always attractive and is along a line connecting the centers of the two masses.
$ \mathbf{F}_{21} $ is the force applied on object 2 by object 1.
Cavendish
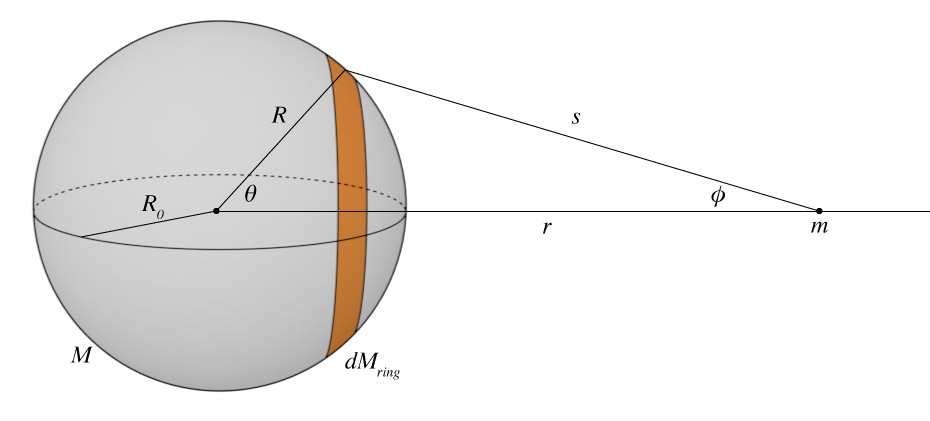
The shell theorem.
The Shell Theorem
Show that a spherical mass (of density $\rho(R)$) acts as a point mass for objects outside.
Consider a mass $m$ a distance $r$ away from the center of a spherical mass $M$. The radius of the spherical mass is $R_0$. First, the force from the ring which a mass $dM$ is:
$$dF_\textrm{ring} = G \frac{m \; dM_\textrm{ring}}{s^2}\cos \phi$$
We can re-express the mass of the ring in terms of its density $\rho(R)$. (The density is at most only a function of the radius, i.e. spherically symmetric)
$$dM_\textrm{ring} = \rho(R) \;dV_\textrm{ring}$$
The volume of a ring is just its thickness: $dR$, times its width: $R d\theta$, times its circumference: $2 \pi R \sin \theta$ which equals:
$$dM_\textrm{ring} = \rho(R) \; 2 \pi R^2 \sin \theta \; dR \;d\theta$$
The $\cos \phi$ can be expressed as:
$$\cos \phi = \frac{r-R\cos \theta}{s}$$
and $s$ can be written as the following (from Pythagorus)
$$ s = \sqrt{ \left( r-R \cos \theta \right)^2 + R^2 \sin^2 \theta} = \sqrt{r^2- 2r R\cos \theta + R^2}$$
Let's put all these back into the force from the ring:
\begin{align*}
dF_\textrm{ring} & = G \frac{m \; dM_\textrm{ring}}{s^2}\cos \phi \\
& = G m \;[ \rho(R) \; 2 \pi R^2 \sin \theta \; dR \;d\theta ] \times [\frac{1}{s^2}] \times \left[\frac{r-R\cos \theta}{s} \right]
\end{align*}
Then, we'll have to integrate over both variables. $dR$ will range from 0 to $R_0$ and $d\theta$ from 0 to $\pi$ to get all the rings that make up the entire sphere.
$$\begin{equation}
F = 2 \pi Gm \left[ \int_0^{R_0} \int_0^{\pi} \frac{\rho(R)\left(r R^2 \sin \theta - R^3 \sin \theta \cos \theta \right)}{\left(r^2 + R^2 - 2 rR \cos \theta \right)^{3/2}}\; d\theta\; dR \right]
\end{equation}$$
Integrating over $\theta$ yields:
$$\begin{equation}
F = \frac{G m}{r^2}\int_O^{R_0} 4 \pi R^2 \rho(R)\;dR
\end{equation}$$
However, the mass of a shell of thickness $dR$ is just:
$$dM_\textrm{shell} = 4 \pi R^2 \rho(R) dR$$
which is just quanity inside the integrand. Thus the force from on shell will be,
$$d F_\textrm{shell} = \frac{G m \; dM_\textrm{shell}}{r^2}$$
This force acts as if it is located at the center of the shell.
We can then integrate over all the mass shells and the above becomes:
$$\begin{equation}
F = G \frac{m M}{r^2}
\end{equation}$$
which is just the equation for the force between two point masses.
little g
$$\begin{equation}
F = G \frac{M_\oplus m}{(R_\oplus+h)^2}
\end{equation}$$
Let's consider the gravitational force a distance $h$ above the surface of the earth. Since $F = ma$, we can see that the acceleration $a$ will be equal to:
$$\begin{equation}
a = G \frac{M_\oplus}{R_\oplus^2} = g
\end{equation}$$
We generally call this value 'little g'.
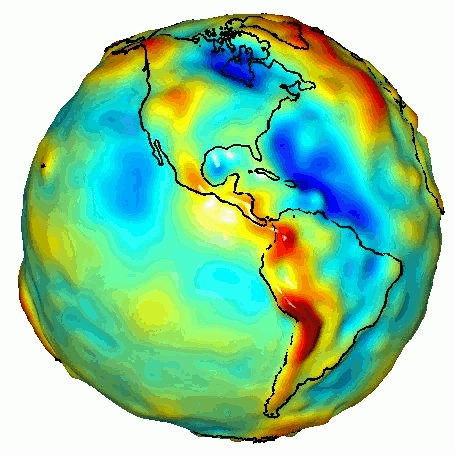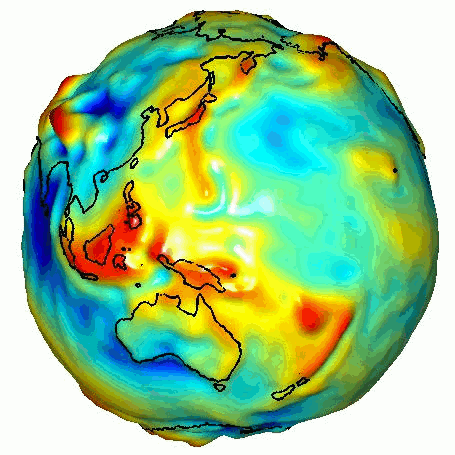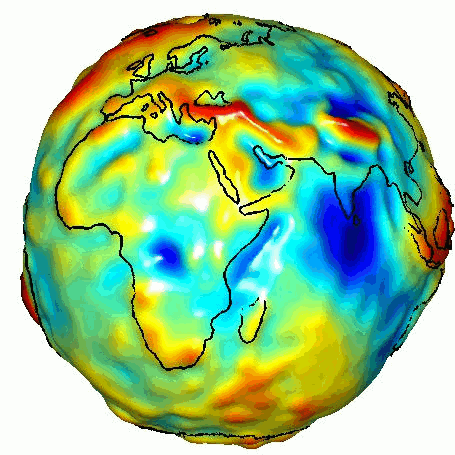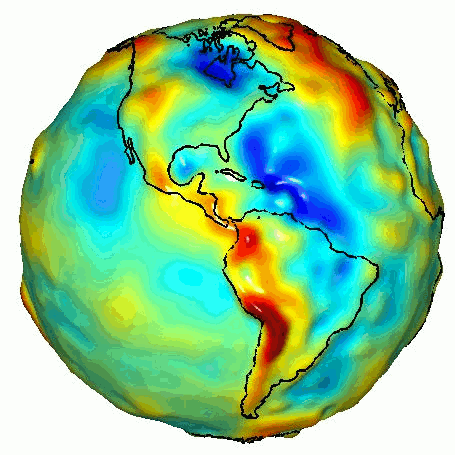
gravity anomalies measured by GRACE
little $g$ is not the same everywhere.
Work and Energy
A point mass $m$ moves from $r_i$ to $r_f$ in a gravitational field.
$$\begin{equation}
U_f - U_i = \Delta U = - \int_{\mathbf{r}_i}^{\mathbf{r}_f} \mathbf{F} \cdot d \mathbf{r}
\end{equation}$$
The change in potential energy is given by the negative of the work done by gravity. Expressing it in the integral above allows for changing force as a function of position (in contrast to the elementary definition: $W = \mathbf{F} \cdot \mathbf{d})$
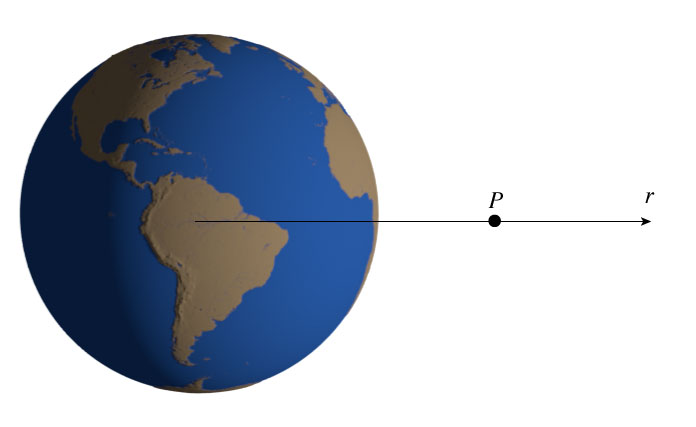
What is the potential energy at point $P$?
Find the work done on an object by gravity as it moves from point $P$ to infinity, where the potential energy is defined as 0.
$$W = \int_R^\infty \mathbf{F(r)} \cdot d\mathbf{r}$$
The force is always against the displacement, so
$$\mathbf{F(r)} \cdot d\mathbf{r} = -\frac{G M_E m}{r^2} dr$$
We can pull the constants out of the integral, and we are left with something very simple to integrate:
$$W = - G M_E m \int_R^\infty \frac{1}{r^2}dr = \left[ \frac{G M_E m}{r} \right]^\infty_R$$
Evaluating at the limits of $\infty$ and $R$, we see that the work done is:
$$W = \left[ \frac{G M_E m}{r} \right]^\infty_R = 0 - \frac{G M_E m }{R} = - \frac{G M_E m }{R}$$
From the original definition of work and potential energy:
$$\Delta U = U_f - U_i = -W$$
thus, since $U_\infty = 0$ we can say: $U = W$
And now we have a potential energy function for masses at a distance $r$ from the center of the Earth:
$$\bbox[15px,border:2px solid red]{U = -\frac{GM_e m}{r}}$$
Potential Plot
The potential energy as a function of position for a body in a gravitational interaction.
Escape Speed
How fast to get something to reach infinity, (and stop there)?
$$\begin{equation}
E = \frac{1}{2}mv^2 - G \frac{M m}{r}
\end{equation}$$
This is the total energy of a particle: kinetic plus potential. Since the particle will be at $r = \infty$ and will have stopped then the total energy must be zero. However, due to conservation of energy, the total mechanical energy will be the same. Thus, $\frac{1}{2}mv^2 - G \frac{M m}{r} = 0$ at all times. Or:
$$\begin{equation*}
\frac{1}{2}mv^2 = G \frac{M m}{r}
\end{equation*}$$
which leads to
$$\begin{equation}
v_\textrm{escape } = \sqrt{\frac{2 G M}{r}}
\end{equation}$$
For Earth, $v_\textrm{escape}$ = 11182.4 m/s. Apollo 11 traveled at 10423 m/s [nasa ref ]. It got a little help from the moons gravity too.
Cartesian & Polar Coordinates
Polar Coordinates $r$ and $\theta$.
In polar coordinates, we have different unit vectors: $\hat{\boldsymbol{\theta}}$ and $\hat{\bf{r}}$.
$$\begin{equation}
\hat{\bf{r}} = \hat{\bf{i}} \cos \theta + \hat{\bf{j}} \sin \theta
\end{equation}$$
and
$$\begin{equation}
\hat{\boldsymbol{\theta}} = - \hat{\bf{i}} \sin \theta + \hat{\bf{j}} \cos \theta
\label{eq:thetahatder}
\end{equation}$$
We can also express some derivatives:
$$\begin{equation}
\frac{d \hat{\bf{r}}}{d\theta} = -\hat{\bf{i}} \sin \theta + \hat{\bf{j}} \cos \theta = \hat{\boldsymbol{\theta}}
\end{equation}$$
$$\begin{equation}
\frac{d \hat{\boldsymbol{\theta}}}{d\theta} = - \hat{\bf{i}} \cos \theta - \hat{\bf{j}}\sin \theta = - \hat{\bf{r}}
\end{equation}$$
And using the chain rule, we can also express time derivatives:
$$\begin{equation}
\frac{d \hat{\bf{r}}}{dt} = \frac{d \hat{\bf{r}}}{d \theta} \frac{d\theta}{dt} = \hat{\boldsymbol{\theta}}\frac{d\theta}{dt}
\end{equation}$$
$$\begin{equation}
\frac{d \hat{\boldsymbol{\theta}}}{dt} = \frac{d \hat{\boldsymbol{\theta}}}{d \theta} \frac{d \theta}{dt}= - \hat{\bf{r}}\frac{d \theta}{dt}
\end{equation}$$
These will be useful later.
2nd Law
To prove the second law, we can show how Conservation of Angular Momentum results in the equal areas in equal times statement.
Angular Momentum Conservation →
Equal Areas in Equal Times →
Angular Momentum
\begin{equation}
\overrightarrow{\mathbf{L}} = \overrightarrow{\mathbf{r}} \times \overrightarrow{\mathbf{p}}
\end{equation}
where $ \overrightarrow{\mathbf{p}} = m \overrightarrow{\mathbf{v}}$
Take the time derivative of $ \overrightarrow{\mathbf{L}}$
\begin{equation}
\frac{d \overrightarrow{\mathbf{L}}}{dt} = \frac{d \overrightarrow{\mathbf{r}}}{dt} \times \overrightarrow{\mathbf{p}} + \overrightarrow{\mathbf{r}} \times \frac{d \overrightarrow{\mathbf{p}}}{dt} = \overrightarrow{\mathbf{v}} \times m \overrightarrow{\mathbf{v}} + \overrightarrow{\mathbf{r}} \times m \frac{d \overrightarrow{\mathbf{v}}}{dt}
\end{equation}
But, this is quickly seen to be zero for a central force:
\begin{equation}
\frac{d \overrightarrow{\mathbf{L}}}{dt } = 0
\end{equation}
\begin{equation}
\overrightarrow{\mathbf{L}} = \overrightarrow{\mathbf{r}} \times m \overrightarrow{\mathbf{v}} = m r v_t \hat{\bf{k}} = L \hat{\bf{k}}
\end{equation}
Motion's of an orbiter during a short time interval $\Delta t$
The total area is the sum of the two triangles:
\begin{equation}
\Delta A \approx \frac{1}{2}r (v_t \Delta t) + \frac{1}{2}(v_r \Delta t) (v_t \Delta t)
\end{equation}
Thus, in the limit of $r \gg v_r \Delta t$:
\begin{equation}
\Delta A \approx \frac{1}{2}r (v_t \Delta t)
\end{equation}
Next, take the time derivative of the changing area:
\begin{equation}
\frac{dA}{dt} = \frac{1}{2} r v_t = \frac{1}{2}\frac{L}{m}
\end{equation}
which shows the area in a given time is constant.
1st Law - Ellipses
The angular momentum per unit mass will be given by:
$$\begin{equation}
\frac{L}{m }= r^2 \frac{d \theta}{dt}
\label{eq:angularmomentumtheta}
\end{equation}$$
and the centrally directed gravitational force is given by:
$$\begin{equation}
\overrightarrow{\bf{F}}= - \frac{G M m}{r^2}\hat{\bf{r}} = m \frac{d \overrightarrow{\mathbf{v}}}{dt}
\end{equation}$$
The acceleration of the orbiting body is therefore:
$$\begin{equation}
\mathbf{a} = \frac{d \overrightarrow{\mathbf{v}}}{dt} = -\frac{GM}{r^2}\hat{\bf{r}}
\label{eq:acceleration-gravity}
\end{equation}$$
but
$$\begin{equation}
\hat{\bf{r}}=-\left( \frac{d\theta}{dt}\right)^{-1} \frac{d \hat{\boldsymbol{\theta}}}{dt}
\label{eq:runitintermsoftheta}
\end{equation}$$
We can put eq \eqref{eq:runitintermsoftheta} into the acceleration equation \eqref{eq:acceleration-gravity}
$$\begin{equation}
\frac{d \overrightarrow{\mathbf{v}}}{dt} = \frac{GM}{r^2}\left( \frac{d\theta}{dt}\right)^{-1} \frac{d \hat{\boldsymbol{\theta}}}{dt}
\end{equation}$$
Combining this with \eqref{eq:angularmomentumtheta}
$$\begin{equation}
\frac{L}{GMm}\frac{d\overrightarrow{\bf{v}}}{dt} = \frac{d \hat{\boldsymbol{\theta}}}{dt}
\end{equation}$$
Integrating both sides of this equation yields:
$$\begin{equation}
\frac{L}{GMm}\overrightarrow{\bf{v}} = \hat{\boldsymbol{\theta}} + \overrightarrow{\bf{e}}
\end{equation}$$
The $\overrightarrow{\bf{e}}$ is a constant of integration that depends on the initial conditions, which we may choose.
The initial conditions of an orbiting body.
We'll say that at $t = 0$, the orbiter is at perihelion and we can orient the axes so that its motion is entirely in the +y direction, in other words: $\overrightarrow{\bf{e}} = e \hat{\bf{j}}$ where $e$ is a constant.
Now:
$$\begin{equation}
\frac{L}{GMm}\overrightarrow{\bf{v}} = \hat{\boldsymbol{\theta}} + e \hat{\bf{j}}
\end{equation}$$
We can take the dot product with $\hat{\boldsymbol{\theta}}$ of both sides:
$$\begin{equation}
\frac{L}{GMm}\overrightarrow{\bf{v}} \cdot \hat{\boldsymbol{\theta}} = \hat{\boldsymbol{\theta}} \cdot \hat{\boldsymbol{\theta}} + e \hat{\bf{j}} \cdot \hat{\boldsymbol{\theta}}
\end{equation}$$
Simplifying, using the definitions above (i.e. \eqref{eq:thetahatder}):
$$\begin{equation}
\frac{L}{G M m}v_t = 1 + e \cos \theta
\label{eq:afterthedot}
\end{equation}$$
($v_t$) is the tangential velocity of the orbiter.
From the definition of angular momentum: $\mathbf{L} = \mathbf{r} \times \mathbf{p}$
$$\begin{equation}
m r v_t = L
\end{equation}$$
which when put back into \eqref{eq:afterthedot}, yields:
$$\begin{equation}
\frac{L^2}{G M m^2 r} = 1+ e \cos \theta
\end{equation}$$
or solving for $r$:
$$\begin{equation}
r = \frac{L^2}{G M m^2 \left( 1 + e \cos \theta\right)}
\end{equation}$$
This is just the polar coordinates expression for a conic section.
Third Law
Special Case: Circular orbits
For example, for an object orbiting the earth, we can write:
$$G \frac{M_E m}{r^2} = m \frac{v^2}{r}$$
We can solve this for $v$, the speed of the orbiting object:
$$ v= \sqrt{\frac{G M_E}{r}}$$
Now we can use the gravitational force to calculate the expected period:
$$v = \sqrt{\frac{G M_e}{r}} = \frac{2 \pi r}{T}$$
which can be solved for $T$:
$$T = \frac{2\pi r^{3/2}}{\sqrt{G M_E}}$$
Kepler figured out a version of this relationship before Newton:
$$T \propto r^{3/2}$$
The period is proportional to the three-halfs power of the orbital radius.
General Case (i.e. ellipses)
\begin{equation}
T^2 = \frac{4 \pi^2}{G(M+m)}a^3
\end{equation}
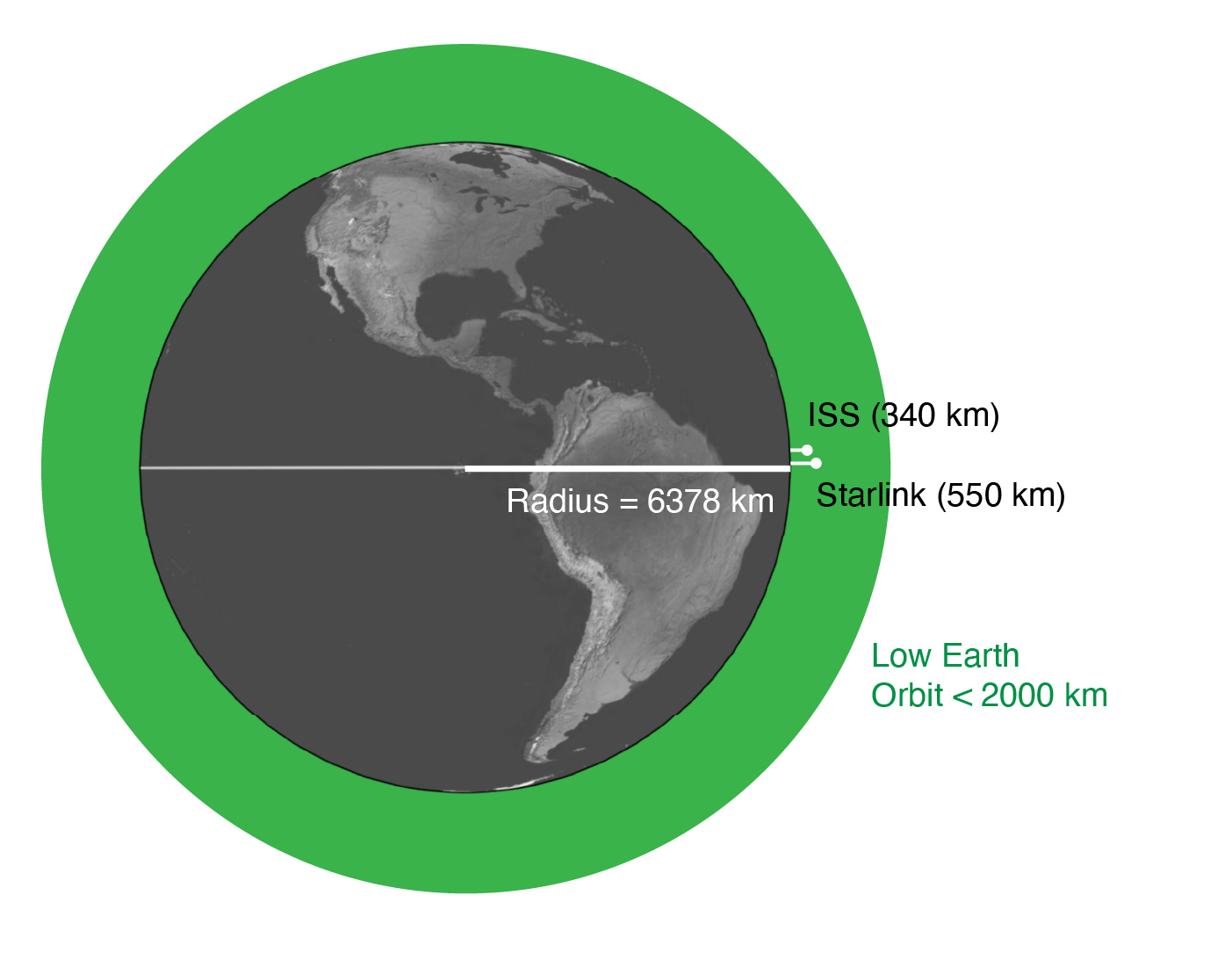
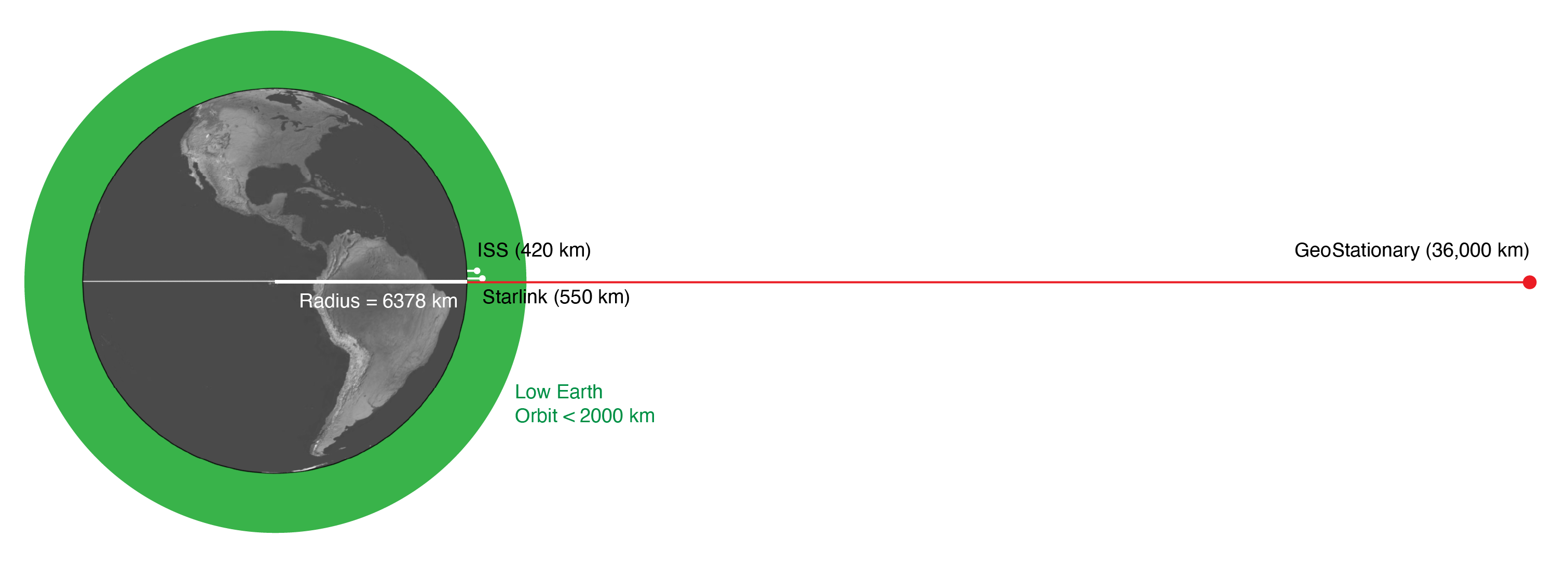
Low Earth
Low Earth Orbit
Most of our satellites are located in Low Earth Orbit. Roughly defined as less than 2000 km above the surface of the Earth.
Orbital Periods there range between 93 minutes and 127 minutes (for circular orbits)
Calc Demo: →
Geostationary
GeoStationary
Earth and Moon
Earth and Moon to scale
Hohmann Transfer Orbit
A typical Homann Transfer Orbit
The semi-major axis of the transfer orbit:
\begin{equation}
a_\textrm{transfer} = \frac{r_e+r_m}{2}
\end{equation}
Lagrange Points
The basic FBD and L1 point
All 5 Lagrange points
Find L1
The sum of forces acting on the earth is equal to its mass time the acceleration, which for an object moving in a circular orbit is centripetal and equal to $v^2/R$:
$$\Sigma F_\textrm{on Earth} = \frac{G M m_E}{R^2} = \frac{m_E v^2}{R}$$
Thus we can say:
$$\frac{GM}{R} = v^2$$
but, based on the relation between speed and period, $T$:
$$v = \frac{2 \pi R}{T}$$
or
$$v^2 = \frac{4 \pi^2 R^2}{T^2}$$
So we can rewrite as:
$$\frac{GM}{R} = \frac{4 \pi^2 R^2}{T^2}$$
Rearranging yields Kepler's Third Law
$$
\begin{equation}
\frac{GM}{R^3} = \frac{4 \pi^2}{T^2}
\end{equation}
$$
Now consider the sum of forces on the satellite:
$$\Sigma F_\textrm{on Sat} = \frac{G M m_\textrm{sat}}{(R-r^2)}-\frac{G m_E m_\textrm{sat}}{r^2} = \frac{m_\textrm{sat}v_\textrm{sat}^2}{(R-r)}$$
This we can simplify to, using Kepler's Third law for the satellite:
$$\frac{GM}{R-r}-\frac{Gm_E(r-R)}{r^2} = v_\textrm{sat}^2 = \frac{4 \pi^2 (R-r)^2}{T_\textrm{sat}^2}$$
or
$$
\begin{equation}
\frac{GM}{(R-r)^3}-\frac{Gm_E}{r^2(R-r)} = \frac{4\pi^2}{T_\textrm{sat}^2}
\end{equation}
$$
Lastly, since we want their periods to be the same: $T_\textrm{sat} = T$
$$\begin{equation}
\frac{GM}{(R-r)^3}-\frac{Gm_E}{r^2(R-r)} = \frac{GM}{R^3}
\end{equation}$$
If we put in the masses of the two major bodies, the Earth and Sun for example, we can calculate the value of $r$ in terms of $R$. For our earth-sun system, the L1 point would be located at
$$r = 0.009969 \; \textrm{AU}$$
or about 1/100 of the earth-sun distance.
Changing signs in the sums of forces could allow to calculate the L2 and L3 positions as well.
The Virial Theorem
The Virial theorem shows that for a gravitationally bound system in equilibrium, the total energy is one-half the time averaged potential energy.
Consider the quantity $Q$.
$$\begin{equation}
Q \equiv \sum_{i} \mathbf{p}_i \cdot \mathbf{r}_i
\end{equation}$$
where $\mathbf{p}_i$ is the linear momentum and $\mathbf{r}_i$ the position of some particle $i$. The product rule gives the following if we take the time derivative of the right hand side.
$$\begin{equation}
\frac{dQ}{dt} = \sum_{i} \left( \frac{d \mathbf{p}_i}{dt} \cdot \mathbf{r}_i + \mathbf{p}_i \cdot \frac{d\mathbf{r}_i}{dt} \right)
\end{equation}$$
We could also say:
$$\begin{equation}
\frac{dQ}{dt} = \frac{d}{dt} \sum_{i} m_i \frac{d \mathbf{r}_i}{dt} \cdot \mathbf{r}_i = \frac{d}{dt} \sum_{i} \frac{1}{2} \frac{d}{dt} \left(m_i r_i^2 \right) = \frac{1}{2}\frac{d^2 I}{dt^2}
\end{equation}$$
where $I$ is the moment of inertia of the total number of particles:
$$\begin{equation}
I = \sum_{i} m_i r_i^2
\end{equation}$$
$$\begin{equation}
\frac{1}{2}\frac{d^2 I}{dt^2} - \sum_{i} \mathbf{p}_i \cdot \frac{d\mathbf{r}_i}{dt} = \sum_{i} \frac{d \mathbf{p}_i}{dt} \cdot \mathbf{r}_i
\end{equation}$$
Now,
$$\begin{equation}
- \sum_{i} \mathbf{p}_i \cdot \frac{d\mathbf{r}_i}{dt} = - \sum_{i} m_i \mathbf{v}_i \cdot \mathbf{v}_i = -2 \sum_{i} \frac{1}{2} m_i v_i^2 = -2 K
\end{equation}$$
Thus:
$$\begin{equation}
\frac{1}{2}\frac{d^2 I}{dt^2} - 2K = \sum_{i} \mathbf{F}_i \cdot \mathbf{r}_i
\label{eq:momInertiaKineticAndClausius}
\end{equation}$$
where we have used the 2nd law of Newton ($\mathbf{F} = \frac{d\mathbf{p}}{dt}$)
Let $\mathbf{F}_{ij}$ represent the force of interaction between two particles in the system. The force on $i$ due to $j$. If you have a particle $i$, then we need to add up the force contributions from every other particle $j$ where $j \neq i$.
$$\begin{equation}
\sum_{i} \mathbf{F}_i \cdot \mathbf{r}_i = \sum_{i} \left(\sum\limits_{\substack{j \\ j\neq i}} \mathbf{F}_{ij} \right) \cdot \mathbf{r}_i
\end{equation}$$
We can re-write the position of the $i$th particle as:
$$\begin{equation}
\mathbf{r}_i = \frac{1}{2}(\mathbf{r}_i + \mathbf{r}_j) + \frac{1}{2}(\mathbf{r}_i - \mathbf{r}_j)
\end{equation}$$
which leads to
$$\begin{equation}
\sum_{i} \mathbf{F}_i \cdot \mathbf{r}_i = \frac{1}{2} \sum_{i} \left(\sum\limits_{\substack{j \\ j\neq i}} \mathbf{F}_{ij} \right) \cdot (\mathbf{r}_i + \mathbf{r}_j) + \frac{1}{2} \sum_{i} \left(\sum\limits_{\substack{j \\ j\neq i}} \mathbf{F}_{ij} \right) \cdot (\mathbf{r}_i - \mathbf{r}_j)
\end{equation}$$
Since the 3rd law of Newton says: $\mathbf{F}_{ij} = - \mathbf{F}_{ji}$, the first term on the R.H.S. in the above equation will be zero.
Thus:
$$\begin{equation}
\sum_{i} \mathbf{F}_i \cdot \mathbf{r}_i = \frac{1}{2} \sum_{i} \sum\limits_{\substack{j \\ j\neq i}} \mathbf{F}_{ij} \cdot (\mathbf{r}_i - \mathbf{r}_j)
\end{equation}$$
Assuming only gravitational interactions:
$$\begin{equation}
\mathbf{F}_{ij}= G \frac{m_i m_j}{r_{ij}^2} \hat{\bf{r}}_{ij}
\end{equation}$$
we can write
$$\begin{align}
\sum_{i} \mathbf{F}_i \cdot \mathbf{r}_i & = - \frac{1}{2} \sum_{i} \sum\limits_{\substack{j \\ j\neq i}} G\frac{m_i m_j}{r_{ij}^3}\left( \mathbf{r}_j- \mathbf{r}_i\right)^2 \\
& - \frac{1}{2} \sum_{i} \sum\limits_{\substack{j \\ j\neq i}} G\frac{m_i m_j}{r_{ij}}
\end{align}$$
The potential energy $U_ij$ between the $i$ and $j$ particles is just the term in the sums:
$$\begin{equation}
U_{ij} = -G\frac{m_i m_j}{r_ij}
\end{equation}$$
Thus,
$$\begin{equation}
\sum_{i} \mathbf{F}_i \cdot \mathbf{r}_i = \frac{1}{2} \sum_{i} \sum\limits_{\substack{j \\ j\neq i}} U_{ij} = U
\end{equation}$$
Now we can fill out eq: \eqref{eq:momInertiaKineticAndClausius}
$$\begin{equation}
\frac{1}{2} \left\langle \frac{d^2 I}{dt^2} \right\rangle - 2 \left\langle K \right\rangle = \left\langle U \right\rangle
\end{equation}$$
where we have replaced all the quantities with the time averaged values.
The average of $\frac{d^2 I}{dt^2} $ is going to be:
$$\begin{align}
\left\langle \frac{d^2 I}{dt^2} \right\rangle & = \frac{1}{\tau} \int_0^\tau \frac{d^2 I}{dt^2} dt \\
& = \frac{1}{\tau} \left( \left. \frac{dI}{dt} \right|_\tau - \left. \frac{dI}{dt} \right|_0 \right)
\end{align}$$
but for periodic motions like orbits:
$$\begin{equation}
\left. \frac{dI}{dt} \right|_\tau = \left. \frac{dI}{dt} \right|_0
\end{equation}$$
So
$$\begin{equation}
\left\langle \frac{d^2 I}{dt^2} \right\rangle = 0
\end{equation}$$
which leads finally to
$$\bbox[15px,border:2px solid red]{-2 \langle K \rangle = \langle U \rangle }$$
or in terms of the total energy $E$
$$\bbox[15px,border:2px solid red]{\langle E \rangle = \frac{1}{2} \langle U \rangle }$$
The Virial Theorem
$$\bbox[15px,border:2px solid red]{-2 \langle K \rangle = \langle U \rangle }$$
or in terms of the total energy $E$
$$\bbox[15px,border:2px solid red]{\langle E \rangle = \frac{1}{2} \langle U \rangle }$$
The Virial Theorem: Uses
It allows for statistical results for many body systems.
For example, with galaxies:
Since $K = \frac{1}{2}Mv^2$ and $U = \frac{GM^2}{R}$, we can obtain:
$$M = \frac{v^2 R}{G}$$
which relates two observable values, $v$ and $R$, with a non observable, but very interesting value, the mass of the galaxy.
The Vis Viva equation
$$v^2 = GM(\frac{2}{r}-\frac{1}{a})$$