Waves
Types of waves

The Great Wave off Kanagawa, Hokusai, 1829
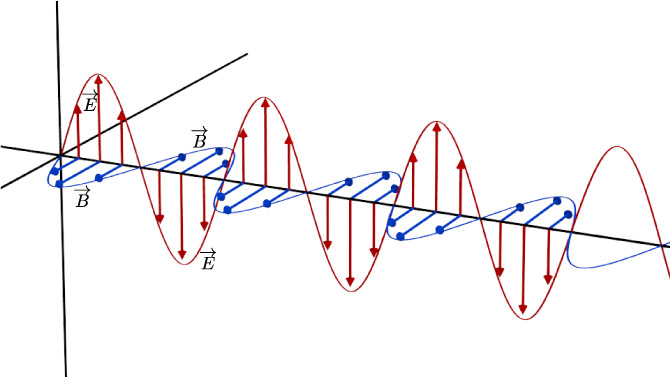
An EM wave

The Quantum Corral
Mechanical Waves
These are the most familiar.
They require a medium.
A wave pulse
A sinusoidal wave
Two types of mechanical waves
Transverse and Longitudinal Waves
There are 2 general classes of waves:
Longitudinal: The Particles move parallel to the direction in which the wave travels.
Transverse: Particles in the medium move perpendicular to the direction that wave is traveling
Imagine one small segment of the rope. Let's look at its motion while the wave is passing through that point.
We'll need to be able to quantify the motion of this little blue region.
Waves, a mathematical formulation
Imagine a small segment of the rope, or spring, or water or whatever medium. To fully describe its motion, we'll need variables which tell us where it is and when -- essentially space and time. If we imagine a rope, which we can say only has two spatial dimensions, then we just need three total variables: $x,y,$ and $t$.
We can therefore completely describe the motion of a segment using: $$y = h(x,t),$$ where $h$ is a function of space and time.
$y$ is simply the transverse displacement of a small element of the string.
A basic wave
Here's a sinusoidal wave traveling in the $+x$ direction.
The dot shows one element of the medium oscillating up and down, sinusoidally.
So, let's use a sine function to describe the position of a small section of the medium.
$$\bbox[10px,border:2px solid red]{y(x,t) = A \sin (kx - \omega t)}$$
Now, we have 3 variables in one function. This means that in order to plot this on a 2D graphs, we'll need to keep one variable constant.
Depending on which one, we'll end up with two different representations of the same wave.
Amplitude
Here we refer to the maximum displacement of the elements away from their equilibrium positions.
This plot shows two waves with amplitudes which differ by a factor of two.
Wavelength
Let's take a sine wave at time $t = 0$. Our previous formula will then be:
$$y(x,0) = A \sin (kx)$$Now, the displacement is the same at both ends of the wavelength
$$ \begin{eqnarray} A \sin (kx_1) & = & A \sin k(x_1+\lambda)\\ & = & A \sin (kx_1 + k \lambda) \end{eqnarray} $$This can only be true if $$\bbox[10px,border:2px solid red]{k = \frac{2\pi}{\lambda}}$$
We'll call $k$ the wavenumber, which we can see is inverse to the wavelength.
Period and Frequency
The wavelength and wavenumber gave us spatial information about the wave. What about temporal?
$$\bbox[10px,border:2px solid red]{f = \frac{1}{T} = \frac{\omega}{2 \pi}}$$.
What should the horizontal axis be labeled as?
- Position
- Time
- Amplitude
- Something else
Vectors are attached to several particles on this wave. What vectors are shown?
- Displacement
- Velocity
- Acceleration
- Force

The velocity of a segment.
$$y(x,t) = A \sin (kx - \omega t)$$
Here is our position equation for the material of the wave. If we wanted to find the velocity of a given point, we would just need to take the time derivative of this equation.
Here is a snapshot of a traveling wave on a rope. It's moving in the $-x$ direction. Which of the labeled segments has the largest negative y-velocity value?

E. All have zero y-velocity values.
Here is a snapshot of a traveling wave on a rope. It's moving in the $- x$ direction. Which of the labeled segments has the largest positive y-acceleration value?

E. All have zero y-acceleration values.
Here is a history graph for a segment of rope. A wave is traveling in the $+x$ direction and the rope is being deformed in the $y$ axis. What is the wavelength of the wave?
- 1 m
- 1.5 m
- 2 m
- 3 m
- Cannot be determined from the information given
What is the frequency, $f$, of the wave?
- .5 Hz
- 2/3 Hz
- 1.5 Hz
- 3 Hz
- Cannot be determined from the information given
Speed of a traveling wave
If we think about the crest of the wave as it moves, its displacement in the $y$ axis is constant.
For that to be the case, the argument of the sinusoidal term must be constant as well.
$$y(x,t) = A \sin (\;\underbrace{kx - \omega t}_{\textrm{constant}}\;)$$
or, $kx - \omega t = \textrm{constant}$
Let's take the time derivative of that equation: $$k \frac{dx}{dt} - \omega = 0$$ -or- $$\frac{dx}{dt} = v = \frac{\omega}{k}$$
rewriting in more familiar terms:
$$\bbox[10px,border:2px solid red]{v = \lambda f}$$
Wave speed on a real string.
What determines the speed of a traveling wave on a stretched string?
We could show by looking at the tensions in the string that the velocity must be determined by the tension, $\tau$, and the linear density, $\mu$. $$\bbox[10px,border:2px solid red]{v = \sqrt{\frac{\tau}{\mu}}}$$
Derive the wavespeed
Which of the following actions would make a pulse travel faster down a stretched string?
- Use a heavier string of the same length, under the same tension.
- Use a lighter string of the same length, under the same tension.
- Move your hand up and down more quickly as you generate the pulse.
- Move your hand up and down a larger distance as you generate the pulse.
- Use a longer string of the same thickness, density, and tension.
A thick heavy (i.e. not massless)rope is hanging from a very tall ceiling. A person grabs the end of the rope and begins moving it back and forth with a constant amplitude and frequency. A transverse wave moves up the rope. Which of the following statements describing the speed of the wave is true?
- The speed of the wave decreases as it moves upward.
- The speed of the wave increases as it moves upward.
- The speed of the wave is constant as it moves upward.
- The speed of the wave does not depend on the mass of the rope.
- The speed of the wave depends on its amplitude.
A wave travels along a string at speed $v_0$ . What will the speed be if the string is replaced by one made of the exact same material, but having twice the radius. (The tension is the same)
A sinusoidal wave with an amplitude of 1.00 cm and a frequency of 100 Hz travels at 200 m/s in the positive x-direction. At t=0s, the point x = 1.00 m is on a crest of the wave.
- Determine $A, v, \lambda, k, f, \omega, T, \textrm{ and } \phi$ for this wave.
- Write the equation for the wave's displacement as it travels.
Energy
An interesting aspect of waves is that they are a means of transferring energy, but not matter.

Here is a frame from the earlier animation. The vectors show the velocity of each element of mass, $dm$. At the crest, ②, the velocity is zero. While, at the $y = 0$ point, ①, the velocity will be a maximum.
Kinetic energy is given by the square of the velocity, thus we can see that the K.E. of the $dm$ element will oscillate between a minimum and maximum during the wave travel.

Energy, cont'd
We should also consider the potential energy of the element $dm$.
At point ②, the string is not stretched at all, while at point ①, the string length is elongated as it passes through the origin. This change in length will change the elastic potential energy.

Quantify energy
The kinetic energy of a particle in motion is given by $KE = \frac{1}{2}m v^2$. In the case of a little section of a rope, $dm$, we write: $$dK = \frac{1}{2}dm \dot{y}^2$$ ($\dot{y} = \frac{dy}{dt}$ which is the time derivative of $y$, or speed in the transverse direction)
Going back to our original definition for the $y$ displacement: $y(x,t) = A \sin\left(kx - \omega t\right)$, we can see that $\dot{y}$ is just: $$\dot{y} = -A\omega \cos\left(kx - \omega t\right)$$
Therefore, our dK can be written: $$dK = \frac{1}{2} dm (-A\omega)^2\cos^2\left(kx - \omega t\right) = \frac{1}{2} \mu dx (-A\omega)^2\cos^2\left(kx - \omega t\right) $$
Quantify energy
If we continue, and take the derivative of dK with respect to time: $$\frac{dK}{dt} = \frac{1}{2} \mu v A^2\omega^2\cos^2\left(kx - \omega t\right)$$
Now, the kinetic energy of one little element is clearly changing all the time, but we can consider the average change in kinetic energy: $$\left(\frac{dK}{dt}\right)_\textrm{avg} = \frac{1}{2} \mu v A^2\omega^2\left[\cos^2\left(kx - \omega t\right)\right]_\textrm{avg}$$
The last term: $\left[\cos^2\left(kx - \omega t\right)\right]_\textrm{avg}$ is equal to $\frac{1}{2}$, so in the end, for the average rate of kinetic change: $$\left(\frac{dK}{dt}\right)_\textrm{avg} = \frac{1}{4} \mu v A^2\omega^2$$
The wave also transmits elastic potential energy (since the rope is kinda springy). This should be equal to the average kinetic energy since they are conserved quantities. Thus, the total rate of energy transmission (aka Power) will be twice what we figured for the kinetic energy: $$\bbox[10px,border:2px solid red]{ P_\textrm{avg}= \frac{1}{2} \mu v A^2\omega^2 }$$
The wave equation
This: $y(x,t) = A \sin (kx - \omega t)$ was just a specific case of a wave. (A sinusoidal traveling wave). We'll need a more general wave equation which can be used to describe any travelling wave.
**Derive** $$\bbox[10px,border:2px solid red]{ \frac{\partial^2 y}{\partial x^2}=\frac{1}{v^2}\frac{\partial^2 y}{\partial t^2}}$$ Derive the wave equationSound waves
A bell is ringing inside of a sealed glass jar that is connected to a vacuum pump. Initially, the jar is filled with air at atmospheric pressure. What does one hear as the air is slowly removed from the jar by the pump?
- The sound intensity gradually increases.
- The sound intensity gradually decreases.
- The sound intensity of the bell does not change.
- The frequency of the sound gradually increases.
- The frequency of the sound gradually decreases.

Speed of Sound
We saw before that the speed of a wave (transverse) was equal to: $$v = \sqrt{\frac{\tau}{\mu}}$$ In this case, $\tau$ was a type of 'elastic property' while $\mu$ would be classified as an 'inertial property'. i.e. $$ \sqrt{\frac{\textrm{elastic proptery}}{\textrm{inertial property}}} = v$$ These two quantities only made sense in reference to a string, but the speed of other types of waves can be determined by analogous considerations.
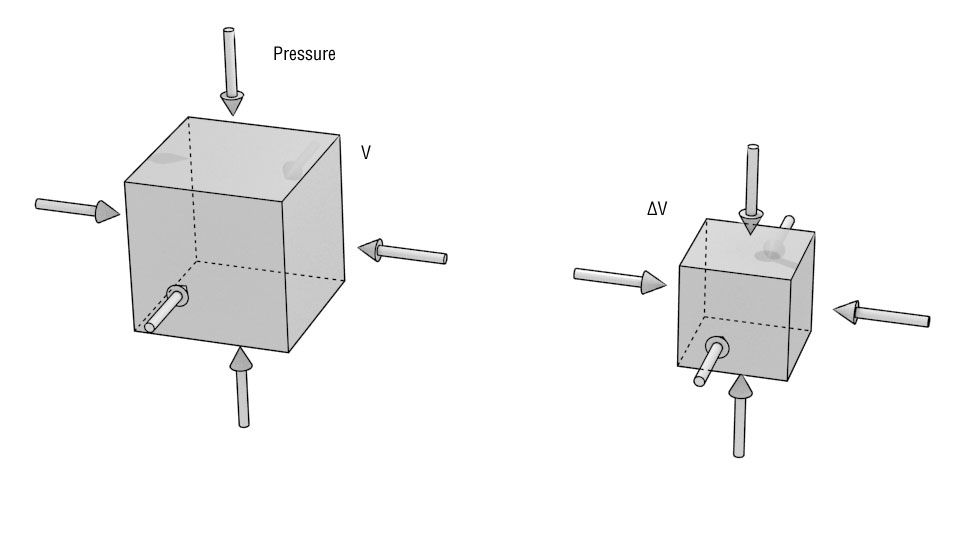
Bulk Modulus
$$\Delta p = - B \frac{\Delta V}{V}$$$B$ is the Bulk modulus of a material. It tells us how the volume of given material will change if pressure is applied to it. Steel for example, has a $B = 1.6 \times 10^{11} $N/m$^2$, while water, which is a bit more compressible, has a $B = 2.2 \times 10^{9} $N/m$^2$
We'll use this parameter to calculate how compression waves travel in a medium (i.e. sound waves)
|
|
v (m/s) |
|
|
|
| Hydrogen (0°C) |
|
| Helium (0°C) |
|
| Air (20°C) |
|
| Air (0°C) |
|
|
|
|
| Sea water |
|
| Water |
|
|
|
|
| Diamond |
|
| Pyrex glass |
|
| Iron |
|
| Aluminum |
|
| Copper |
|
| Gold |
|
| Rubber |
|
Here is a table that lists the velocity of sound in various materials.
The speed of sound is dictated by the material properties of the medium. Just like it was for the string.
$$v_\textrm{sound} = \sqrt{\frac{B}{\rho}}$$
A hammer taps on the end of a 4.00 m long metal bar at room temperature. A microphone at the other end of the bar picks up two pulses of sound, one that travels through the metal and one that travels through the air. The pulses are separated in time by 9.00 ms. What is the speed of sound in this metal?
You are observing a thunderstorm. In the distance, you see a flash of lightning. Five seconds later, you hear thunder. How far away was the lightning flash?
- 1 mile (1.6 km)
- .5 mile (.8 km)
- 2 miles (3.2 km)
- .25 miles (.4 km)
- 5 miles (8.0 km)
Traveling Sound Waves

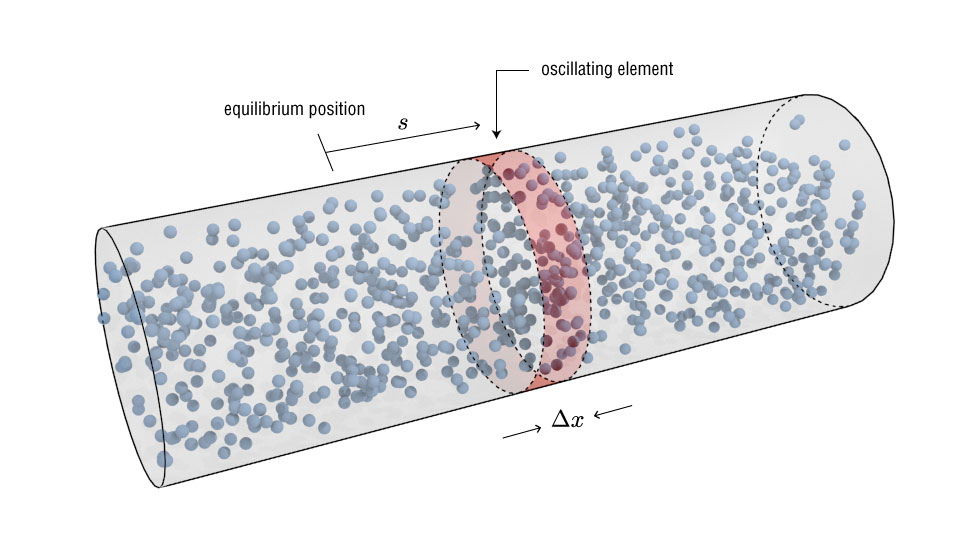
To describe the longitudinal motion of an element of the medium, we can use a sinusoidal function:
$$s(x,t) = s_m \cos (kx - \omega t)$$All of our wave parameters are still present: $f, \lambda, \omega, k, T$
However, it's easier to work with pressure, $p$.

The volume of our element will just be the length times its cross-sectional area: $$V = A\Delta x. $$ While the change in volume of this element will be given by: $$\Delta V = A \Delta s.$$
We can substitute these back into our formula for the bulk modulus: $$\Delta p = -B\frac{\Delta s}{\Delta x} = -B\frac{\partial s}{\partial x}$$
Thus, we can see the pressure at a given location oscillates with time.
Graphical Representation of sound waves
We'll see plots like this a lot. Here we have a speaker producing a sound wave. We'll plot the displacement of the elements of air as a function of position.
A particle of dust is floating in the air approximately one half meter in front of a speaker. The speaker is then turned on produces a constant pure tone of 267 Hz, as shown. The sound waves produced by the speaker travel horizontally. Which one of the following statements correctly describes the subsequent motion of the dust particle?
- The particle of dust will oscillate in the $\pm x$ direction with a frequency of 267 Hz.
- The particle of dust will oscillate in the $\pm y$ with a frequency of 267 Hz.
- The particle of dust will be accelerated toward the right ($+x$) and continue moving in that direction.
- The particle of dust will move toward the right (+$x$) at constant velocity.
- The dust particle will remain motionless as it cannot be affected by sound waves.
Radially Propagating Waves
Here is our standard, circular wave pattern.

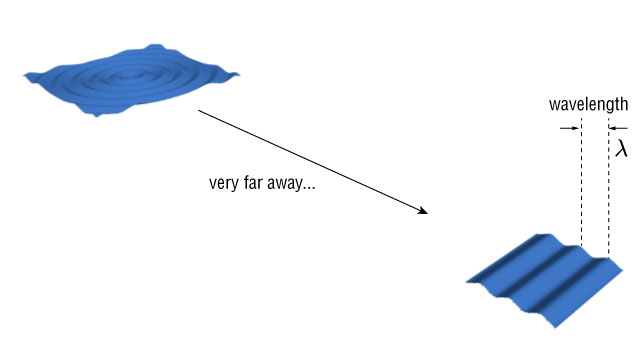
We can approximate the circular waves as parallel wave fronts if we are far enough away from the source. (far would mean $d \gg \lambda$).
Wave fronts
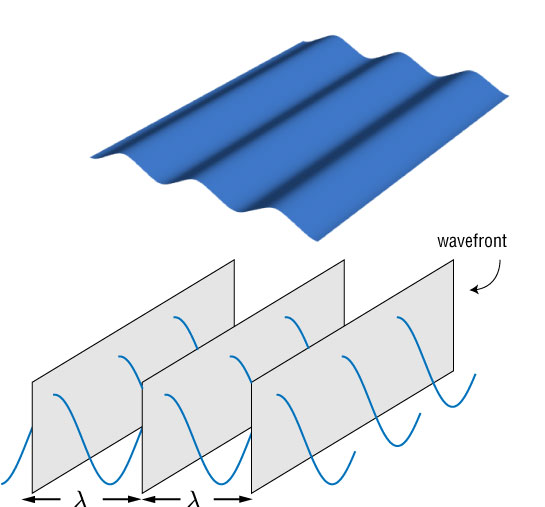
A wave front
We'll consider an intensity, $I$, to describe and quantify the loudness of the waves. $$I = \frac{P}{A}$$ Here, $P$, is the rate of energy transfer (power) and $A$ is the area over which we are considering.
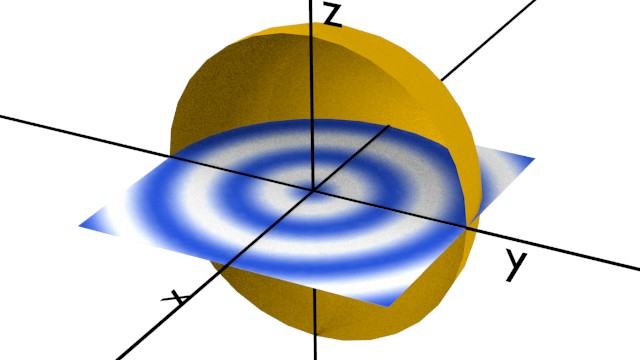
To find the power at some distance, $r$, from the source, we need to use the surface area of a sphere at that distance: $$I = \frac{P}{A} = \frac{P}{4 \pi r^2}$$
Nancy is a distance d in front of a speaker emitting sound waves. She then moves to a position that is a distance 2d in front of the speaker. By what percentage does the sound intensity decrease for Nancy between the two positions?
- 10%
- 25%
- 50%
- 75%
- The sound intensity remains constant because it is not dependent on the distance.
Intensity
To quantify how loud a given sound is, we'll define a term $\beta$: the sound intensity level. It is calculated by comparing the intensity of the sound in question, $I$, to a base level, the threshold of hearing: $I_0$.
$$\beta = (10 dB) \log \frac{I}{I_0}$$The threshold of hearing $I_0$ defined as $I_0 = 1.0 \times 10^{-12} \;\rm W/m^2$
The units of $\beta$ are given in decibels.
If a sound has an intensity of $1.0 \times 10^{-12} \;\rm W/m^2$, then we can see that it will have an intensity level of 0 dB.
$$\beta = (10 \textrm{dB})\log_{10}\frac{I_0}{I_0} = (10 \textrm{dB}) \log_{10}(1) = 0 \; \rm dB$$
A very loud sound, one that might damage your ears, can have an intensity of 10 W/m$^2$. How many decibels is that?
| Sound | $\beta$ (dB) | $I$ W/m$^2$ |
|---|---|---|
| Threshold of Hearing | 0 | $1.0 \times 10^{-12}$ |
| A Whisper at 1m | 20 | $1.0 \times 10^{-10}$ |
| Conversation at 1m | 60 | $1.0 \times 10^{-6}$ |
| Vacuum Cleaner | 80 | $1.0 \times 10^{-4}$ |
| Home Stereo | 110 | 0.1 |
| Threshold of PAIN | 130 | 10 |
We can see that there is wiiiide range of intensities heard during a normal day out and about. That is why it makes more sense to use a log scale when describing this phenomenon.
If the sound intensity level at distance d of one trombone is $\beta$ = 70 dB, what is the sound intensity level of 99 identical trombones, all at distance $d$?

The Grateful Dead and their crew built a speaker system that was able to generate 26,400 Watts of audio power. It was called the Wall of Sound. How many decibels would this make at ¼ mile away from the stage? (Assume an isotropic sound distributioin)
Doppler
General Doppler Shift
$$f' = f \frac{v \pm v_D}{v \pm v_S}$$- $f$ = emitted frequency
- $f'$ = detected frequency
- $v$ = speed of sound in air
- $v_D$ = speed of detector
- $v_S$ = speed of source
When the motion of detector or source is toward the other, the sign on its speed must give an upward shift in frequency. When the motion of detector or source is away from the other, the sign on its speed must give a downward shift in frequency.
A child is swinging back and forth with a constant period and amplitude. Somewhere in front of the child, a stationary horn is emitting a constant tone of frequency $f$. Five points are labeled in the drawing to indicate positions along the arc as the child swings. At which position(s) will the child hear the lowest frequency for the sound from the horn?
- at 2 when moving toward 1
- at 2 when moving toward 3
- at 3 when moving toward 2
- at 3 when moving toward 4
- at both 1 and 4
A 2kHz sine wave generator is swung around in a circle with a rope of length 1m at a speed of 100 rotations per minute. Find the highest and lowest frequencies heard by stationary listeners out side the circle but in the plane of rotation.